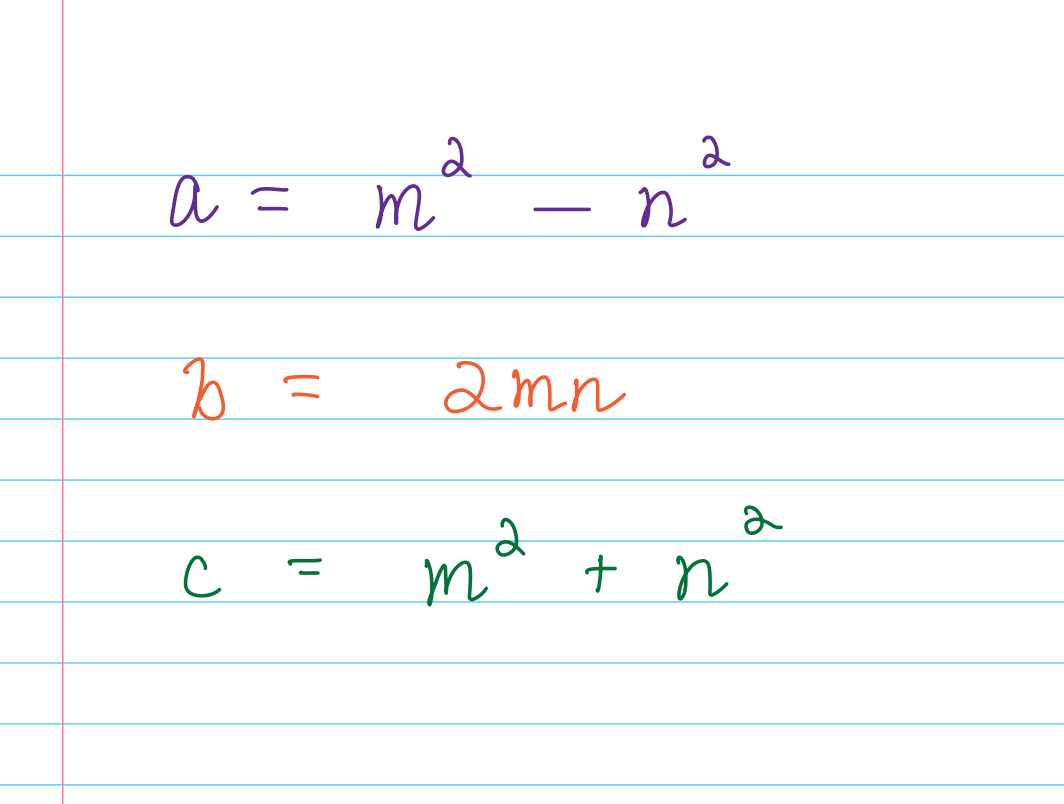The One Thing Everyone Remembers From Math Class

How to Not Suck at Math, part 11

This is my series on how to get better at math.

Previous posts in the series:

Part 1: Addition and Subtraction

Part 2: Multiplication, Division, and Fractions

Part 3: The Major Key of Mathematical Fluency

Part 4: A Proof for this Approach to Numeracy

Part 5: “I’m Just Not A Math Person!”

Part 6: How the Sign Rules Work, and Why

Part 7: The Box Method of Multiplication

Part 8: Elite Mathematical Training

Part 9: An Extremely Cool Math Trick

Part 10: The One Where Algebra Starts Making Sense

Posts 1-5 are not behind the paywall. Parts 6 and beyond are, but this link will give you 10% off. If you’d like to get them but can’t afford a paid subscription, email me at hollymathnerd at gmail dot com and I’ll give you a free one.

---

Comments are normally open for paid subs, but I have a hellish week at work starting in a couple of hours and need all my energy for that so they’re going to be closed pretty quickly this time, sorry!

---

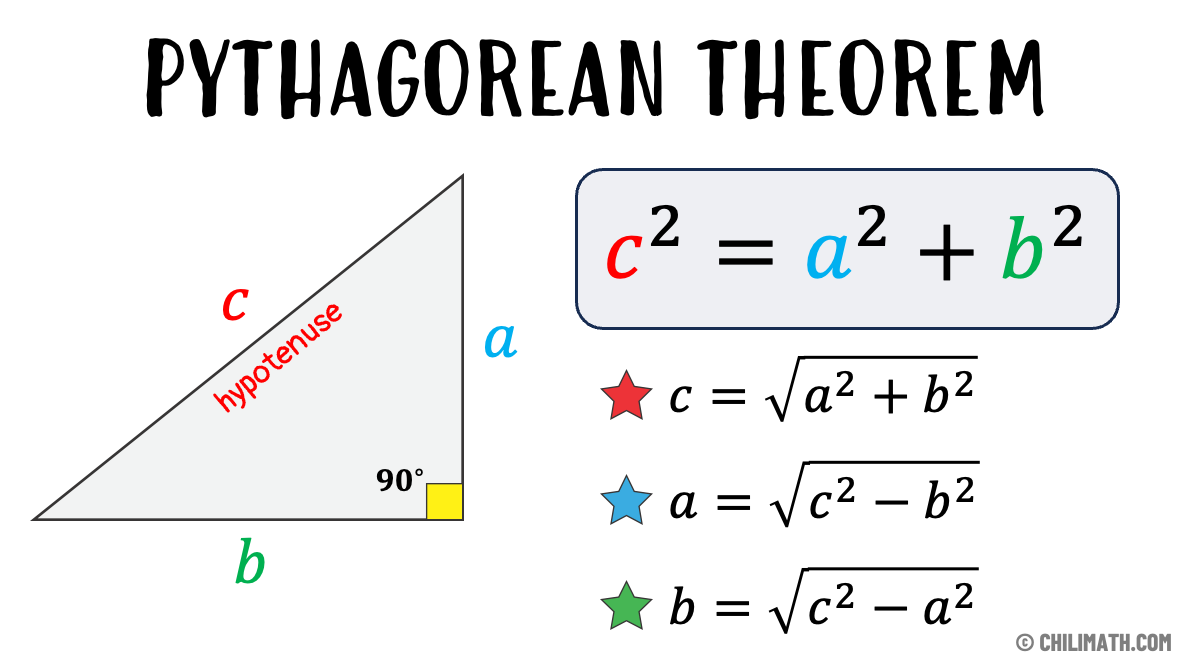
“A Squared Plus B Squared Equals C Squared”

The one thing everyone remembers from high school trigonometry is the Pythagorean theorem: how to find the length of the hypotenuse of a right triangle.

Any three numbers that are related to each other by the Pythagorean theorem — three numbers for which the equation is true — are called a “pythagorean triple.”

Here are some Pythagorean triples.

These are called primitive Pythagorean triples because the a and b terms have no factors in common other than 1, a condition we call “coprime.”

The factors of 3 are 1 and 3. The factors of 4 are 1, 2, and 4. So 3 and 4 are coprime.

The factors of 13 are 1 and 13. The factors of 84 are 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, and 84. So 13 and 84 are coprime.

Any primitive Pythagorean triple can simply be multiplied to create a new one.

Did you know that there are formulas you can use to generate Pythagorean triples?

There are! You can amaze your kids with this by just applying them, but I’d like to help you actually understand where they come from.

For any pair of positive numbers (m, n) where m is greater than n and (m, n) are coprime (meaning they have no factors in common other than 1), and of opposite parity (which just means that one is even and one is odd), here’s how you can get a primitive Pythagorean triple.

This will work every time.

But why does it work? How can understanding where these rules come from help you understand trigonometry, the mathematics of the relationships of the real world and its objects all around you?