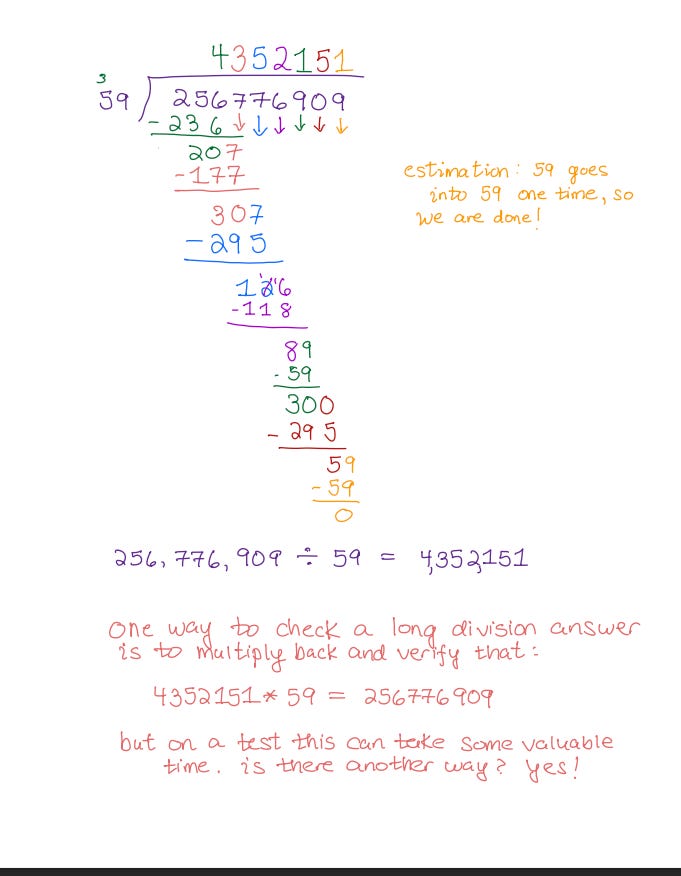How to Not Suck At Math

a guide for helping yourself and your kids (part 2)

---

This post has a lot of pictures and is too long for some email clients; you can read it on the Substack website or in the app.

---

This is part of a new series about how to help yourself or your kids improve in mathematics. It’s based partly on my own experience of having to learn how to learn mathematics, partly on extensive tutoring experience, and partly on many conversations with homeschooling parents, as well as parents struggling to understand Common Core mathematics. Many future editions are already planned, but feel free to leave suggestions for future editions in the comments (open for paid subscribers) or by email to hollymathnerd at gmail dot com.

I may put future editions behind the paywall; I’m not sure yet. If you want to subscribe to be sure you get them all, this link will give you 10% off. If you can’t afford a paid subscription, email me and I’ll give you a free one.

Previous posts in the series:

Part 1: Addition and Subtraction

---

Part 2: Multiplication, Division, and Fractions

First, a refresher. Most of you have been using calculators or apps for years now, so I’m writing out a refresher to help.

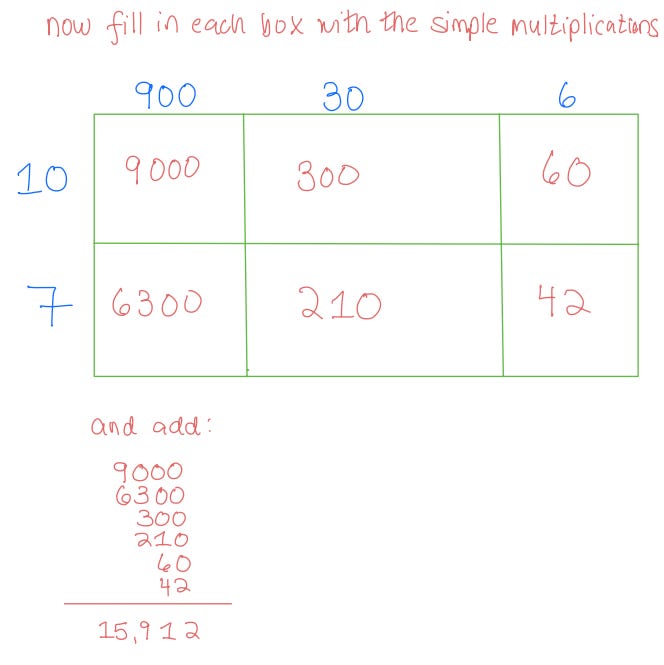
Multiplication (the traditional way and the Common Core/Box way):

The “box” method is how I do multiplication in my head, but I would never teach it to a kid in place of the traditional method. Why?

The traditional method requires more use of the multiplication tables, more complex thought, requires more organizational skills, is more challenging, and also makes it easier to grasp the relationship between the final answer and the two numbers you multiply to get it.

Division Refresher:

Fractions Refresher:

But what ARE multiplication and division?

Multiplication is the mathematical operator for very quickly adding numbers, groups, quantities, etc., of particular sizes. To find the number of eggs in 5 full cartons, one can add:

12 + 12 + 12 + 12 + 12 = 60

Or one can do it very quickly by multiplication, taking the quantity in one carton, 12, and multiplying it by the number of cartons we are concerned with, 5:

12 x 5 = 60.

Division is the mathematical operator for breaking numbers, groups, quantities, etc., into pieces of a particular size.

If you have 60 eggs and need to put them into cartons, you can divide your quantity of eggs, 60, into the number of eggs each carton holds, 12:

60 ÷ 12 = 5.

Do you see already that there’s a relationship between multiplication and division?

That relationship exists because in a very powerful sense, multiplication and division are the same thing.

When we divide into pieces of a particular size, what we are really doing is multiplying by the reciprocal of that size.

What’s a reciprocal? Flipping the numerator and denominator of a fraction.

Because every whole number has a denominator of 1, we can always do this.

This fact is why when you learned to multiply and divide fractions, you learned to do them the exact same way, with one extra step for division: flipping the second fraction (the divisor), first.

Another example:

What This Has Been Building Up To

All of this has been building up to a moment, to try to give you a powerful intuitive “light bulb” that division and multiplication are different aspects of the same thing. Ready?

What do you do if you want to find half of something? Splitting the cost at a dinner check, say? You divide by two.

If there are three of you at dinner and you’re going to split the check equally, each paying one third of the check, what do you do? You divide by three.

If the dinner check is $90 and you are going to pay half OF it, you divide by 2 and get $45.

If there are three of you and you are going to pay one third OF it, you divide by 3 and get $30.

Dividing by 2 and multiplying by one-half get you the same answer.

Dividing by 3 and multiplying by one-third get you the same answer. Why?

OF MEANS MULTIPLY!

Internalize that and help your kids internalize it, too.

OF MEANS MULTIPLY.

You can divide by 2 or multiply by one-half if you want to get one-half OF a quantity.

You can divide by 3 or multiply by one-third if you want to get one-third OF a quantity.

You can divide by 4 or multiply by one-fourth if you want to get one-fourth OF a quantity.

And so on!

Yes, Your Kids Need to Memorize Their Multiplication Tables

Their school is probably not going to make them memorize the multiplication tables, which is a damn shame. You should. If at all possible, I suggest finding a way to incentivize your kids to do this. Don’t turn it into a power struggle that they will not enjoy (and then associate their distress or frustration with math).

You know your kid best. Some kids will go off into a cave and memorize them in two days after being offered a reward. Others would rather memorize them with you, using it as an opportunity for interaction. Motivate your child in the way that works best, but motivate them.

Use their achievement of memorizing their multiplication tables as a way to help them start to make the connection between multiplication and division. Once they know that 12 x 5 = 60, you can work on the understanding that 60 ÷ 5 = 12 and 60 ÷ 12 = 5. The multiplication tables and the corresponding division problems should absolutely be rote for your kids. Automatic. Instantly repeatable without stopping to think.

Why?

Again, this is how you set them up for success in algebra.

When arithmetic is second-nature, they’ll be much more likely to find algebra fun, exciting, and not nearly as challenging as their classmates do.

Part 3: the major key of mathematical fluency — the Fundamental Theorem of Arithmetic.

In a future post: the sign rules. Why negative times negative is positive and the rest of them, with a bit about factoring and the distributive and commutative properties. (Yes, you’ll even know what those words mean!)

---