The Box Method of Multiplication
How to Not Suck at Math, part 7
This is part of a new series about how to help yourself or your kids improve in mathematics. It’s based partly on my own experience of having to learn how to learn mathematics, partly on extensive tutoring experience, and partly on many conversations with homeschooling parents, as well as parents struggling to understand Common Core mathematics. Many future editions are already planned, but feel free to leave suggestions for future editions in the comments (open for paid subscribers) or by email to hollymathnerd at gmail dot com.
The first five posts are not behind the paywall; all future posts will be; this link will give you 10% off. If you’d like to get them but can’t afford a paid subscription, email me at hollymathnerd at gmail dot com and I’ll give you a free one.
Previous posts in the series:
Part 1: Addition and Subtraction
Part 2: Multiplication, Division, and Fractions
Part 3: The Major Key of Mathematical Fluency
Part 4: A Proof for this Approach to Numeracy
Part 5: “I’m Just Not A Math Person!”
Part 6: How the Sign Rules Work, and Why
The Box Method of Multiplication
When COVID started and the entire country became homeschoolers overnight, I offered my help to Twitter followers who needed assistance in doing math with their kids. Over and over, the thing that made people freak out and decide they needed help was the box method of multiplication.
Today I’m going to explain how and why the box method works.
Multiplication can be thought of in two ways; grasp whichever is easier for you. You can think of it as fast adding.
How many eggs are in 7 dozen? Here’s one dozen. You can count the eggs in this picture. How many eggs would there be in 7 of these?
12 + 12 + 12 + 12 + 12 + 12 + 12 = 84.
Or to do this adding a bit faster, invoke the multiplication tables: 12 x 7 = 84.
The second way to think of it as the mathematical process of creating copies. 12 x 7 is seven copies of 12. Seven dozen eggs is seven copies of a dozen eggs, for a total of 84 eggs.
Consider 947 x 17.
times
This is 17 copies of 947, or adding up the contents of 17 boxes that each contain 947 things.
Using a calculator, we get a quick answer: 16,099.
Using the normal multiplication algorithm, we get an answer that looks like this:
The box method of multiplication first splits both numbers into their component parts: 900, 40, and 7 for the 947 and 10, 7 for the 17, leaving boxes to correspond to each combination of the component parts:
The reason for this is to create the simplest possible multiplication problems, things that can be done mentally with ease by anyone who knows the multiplication tables and some simple rules. Simple rules like that multiplying anything at all by 10 is simply taking the number and putting a 0 on the end, by 100 is putting two 0’s on the end—9 x 10 is 90, 75 times 100 is 7500, etc.
Then by adding up the answers from the simpler multiplication, getting a final answer:
Why Does This Work?
Those of you who find mathematics intuitive and are able to think about it fluidly will find this obvious. Those of you who find mathematics scary and confusing will, I hope, have a light bulb moment. I am in the former group now but was in the latter group until I learned how to learn mathematics, so I hope I can explain this well enough for both groups.
The box method works because numbers are a representation of their parts, always. That seems like a tautology, like a statement so obvious you shouldn’t bother saying it, but it really matters.
You understand this with addition. Nearly everyone learned to add this way. What’s 9 + 7? Move over a 1 to make 10, leaving 6. 16. What’s 7 + 8? Move over 3 to make 10, leaving 5. 15.
What’s $1.75 plus 95 cents? Move over 25 cents to make $2.00, leaving 70 cents. $2.70
Or some of you came to understand this working a register at your first job, making change.
The customer’s bill is $8.84. They pay with a $10 bill. You return 16 cents to get them up to $9, and then another $1 to make the $10 they paid you.
The exact same thing is true of multiplication.
Go back to the eggs for a moment. 7 dozen eggs is 84 eggs, because 12 x 7 = 84.
Let’s split the 12 into 10 and 2 for a minute.
7 copies of 10 is 70.
7 copies of 2 is 14.
70 + 14 = 84.
Or go back to thinking of money, ignoring tax (ha ha, if only, right) for the sake of this explanation.
An item costs $2.25. You want to buy 9 of them.
That’s 9 copies of $2, or $18, and 9 copies of 25 cents, or $2.25, for a total of: $20.25.
The box method of multplication takes advantage of the way that numbers can be broken down into simpler parts, using it to take a complicated math problem and breaking it into something easier.
If you’ve ever been impressed by people who can do math in their heads, really give some thought to practicing the box method. It’s easier than it probably seems, and I bet you can do it. Here, I’ll show you.
Don’t reach for your calculator, but just try this one in your head: 15 x 8.
That’s 15, easily split into 10 and 5, times 8.
Taking the 10 component of 15 first, 10 x 8 = 80.
Now take the 5 component of 15: 5 x 8 = 40.
80 + 40 = 120.
Now try this one: 19 x 9.
That’s 19, easily split into 10 and 9, times 9.
Taking the 10 component of 19 first: 10 x 9 = 90.
Now take the 9 component of 19: 9 x 9 = 81.
90 + 81 = 171.
One more, slightly more complicated:
15 x 27.
That’s 15, easily split into 10 and 5, multiplied by 27, easily split into 20 and 7.
Starting with the 10 component of 15:
10 copies of 20 is 200.
10 copies of 7 is 70.
Add those up, you get 270.
Now the 5 component of 15:
5 copies of 20 is 100.
5 copies of 7 is 35.
Add those up, you get 135.
270 + 135 is also pretty simple to do in your head. Recognizing that 270 and 130 add up to 400, it’s 405.
That’s how and why the box method works. I don’t agree with the Common Core practice of teaching kids only this method, because I think there’s a lot of value in the old-fashioned algorithm. But once a kid has that one down, I like the idea of adding the box method. It helps promote a mental fluidity that is useful, in my opinion, and very little is more motivating to most kids than being able to do something in their head that an adult needs a calculator or computer to do.
Anything that motivates kids to get good at math is a plus, in my opinion.
Try to do a few of these in your head, starting with two digits times either one or two digits. As you get better at it, start going for bigger numbers. I think you’ll find this is fun and a kind of mental exercise that makes your day better.
Part 8 is probably going to go into algebra, which is where many people first get the silly notion that they’re not “a math person.” But I’m always open to changing my plans for this series, so if there’s something you’re more interested in, leave a comment or send me an email to hollymathnerd at gmail dot com.








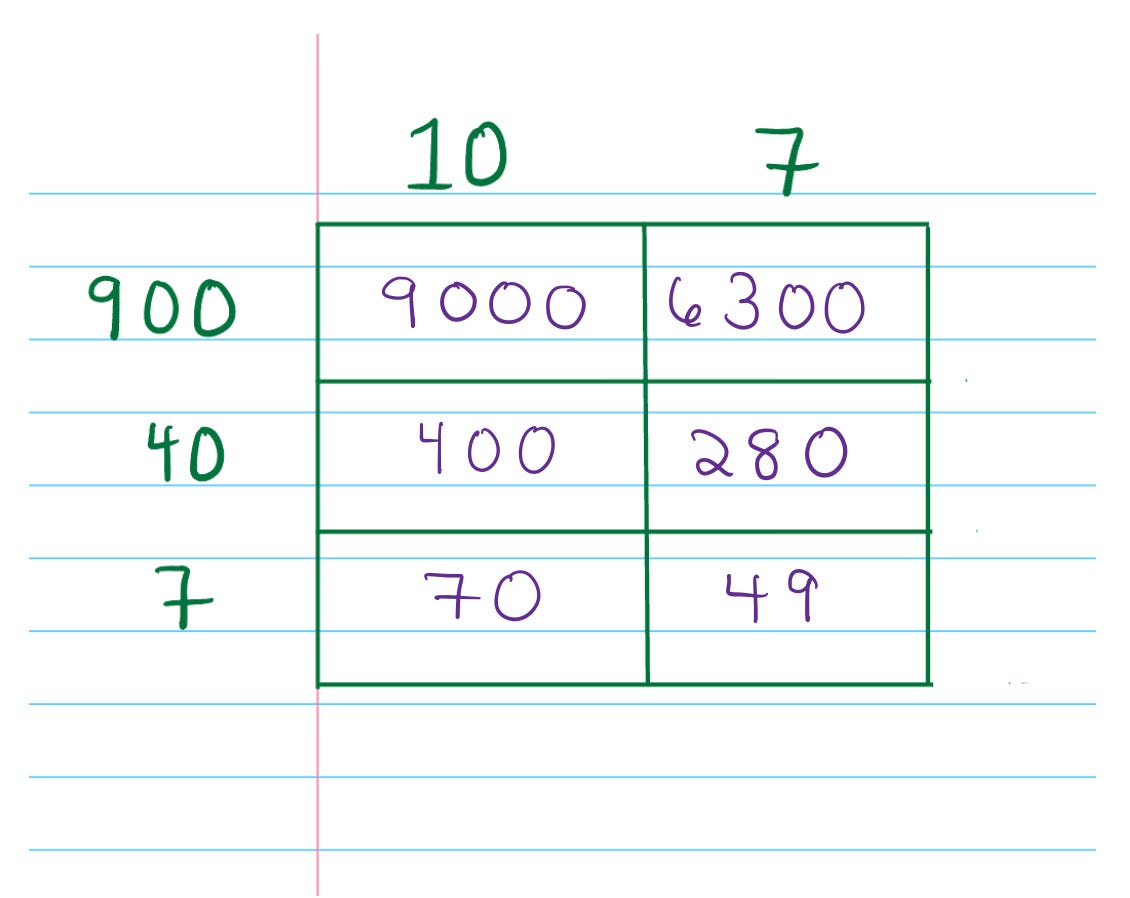
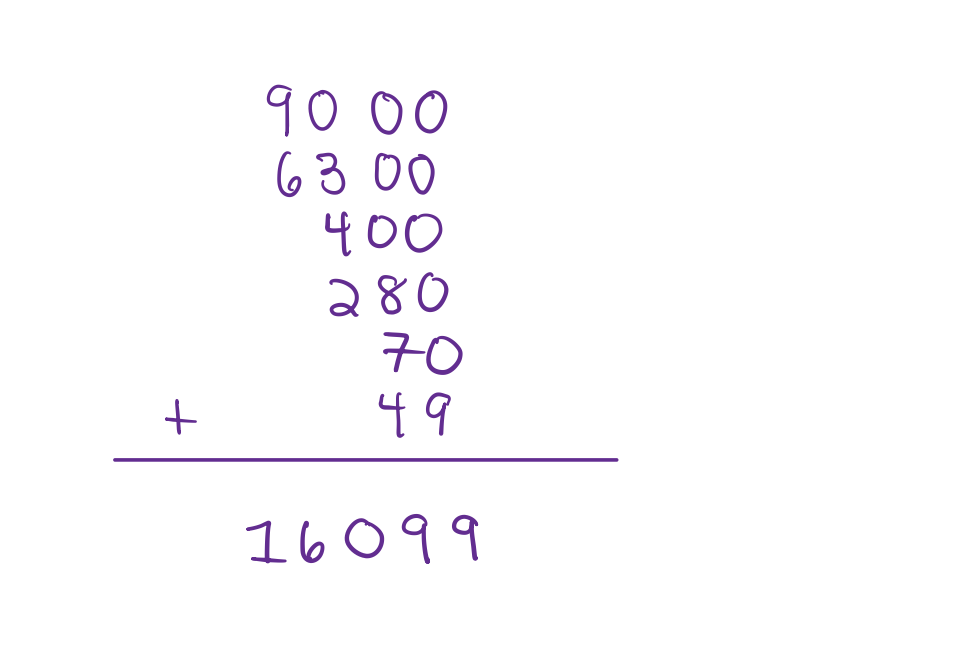
The real question is what is the correct order to take the eggs out of the box as you use them?
I applaud your decision to tackle algebra next, as this would really help me out! I teach ground school to student pilots (and these are often adults in their 30s to 50s who haven't thought about math since they left high school), and the two areas that they really struggle with are weight and balance calculations and solving for the omitted variable in time/distance/speed or time/gallons/fuel burn equations. Both these are much easier to approach if the student is comfortable with translating the words into an algebraic equation, but I have never hit on guidance that works for everyone. Looking forward to your thoughts!