A Proof for This Approach to Numeracy
How to Not Suck At Math, part 4
This post has a lot of pictures and is too long for some email clients; you can read it on the Substack website or in the app.
This is part of a new series about how to help yourself or your kids improve in mathematics. It’s based partly on my own experience of having to learn how to learn mathematics, partly on extensive tutoring experience, and partly on many conversations with homeschooling parents, as well as parents struggling to understand Common Core mathematics. Many future editions are already planned, but feel free to leave suggestions for future editions in the comments (open for paid subscribers) or by email to hollymathnerd at gmail dot com.
I may put future editions behind the paywall; I’m not sure yet. If you want to subscribe to be sure you get them all, this link will give you 10% off. If you can’t afford a paid subscription, email me and I’ll give you a free one.
Previous posts in the series:
Part 1: Addition and Subtraction
Part 2: Multiplication, Division, and Fractions
Part 3: The Major Key of Mathematical Fluency
Part 4: A Proof for This Approach To Numeracy
Twice now, I’ve said the next post would explain the sign rules, and I promise I’ll get to that eventually.
This post will serve to tie together everything I talked about in the first three—how understanding addition, subtraction, multiplication, division, fractions, and the Fundamental Theorem of Arithmetic (part 3) in the manner I’ve described promotes mathematical fluency.
Below are problems from various unit tests in Algebra 1 that I grabbed screenshots of from Khan Academy. Each shows my worked-out answer, explaining how the approach I recommend in the first three parts of this series enables the answer to be found easily and efficiently.
If anything here isn’t clear, please do feel free to leave a comment (open for paid subscribers, and access will be granted to anyone who can’t afford it, just email me).
In part 2, we covered that “of means multiply,” and that’s how I solved this one; completely mentally.
Because I know the multiplication tables quite well, I know that this is something greater than 12 x 12, which is 144. 13 x 13 is easy to do in your head if you know the multiplication tables. 13 x 10 = 130, and 13 x 3 is just 3 more than 12 x 3, or (36 + 3). 169 = 130 + 39. But what about those confusing decimals? 13 x 13 is 169, but this is 1.69 so there’s a decimal in there somewhere. Because I know that “of means multiply,” this one is a cinch. 1.3 copies of 1.3 would be about 1.69, which means 1.3 is the answer!
Factoring, the skill that understanding the Fundamental Theorem of Arithmetic promotes most directly, is highly relevant here. The thought process goes: “216 is even, so divide it by 2 — ah! 2 x 108.”
From there, the multiplication tables kick in if you know them by rote. 108 = 9 x 12.
Then re-write 9 and 12 as their prime decompositions:
Combine like terms:
And pull out the perfect cubes, since this is taking a cube root:
First step: multiply the terms both inside and outside the radicals, but there’s no need to actually do the 18 x 8 part just yet — a conceptual application that the FTOA helps you apply. Products are just combinations of their factors, so if you’re going to factor anyway, you may as well leave things factored!
Now re-write the 8 and 18 as their factors, factors that should jump to mind immediately from knowing the multiplication tables, and then again as their prime decompositions. (If you’ve practiced the prime decompositions and those jump to mind first, it’s totally fine to skip that step.)
Then just combine the like terms and start pulling perfect squares out. This method shows how to use the multiplication tables that are usually memorized to solve problems that go beyond them, too:
Final answer:
Someone who knows their multiplication tables should immediately have 9 x 12 spring to mind for 108, so that’s start with that:
Now to re-write the factors of 9 and 12 as their prime decompositions, which I can do in my head (and so will you and your kids, after a bit of practice) but will write them out here for clarity:
Then it’s a simple matter of applying the exponent rules in reverse. Taking the square root of something squared, as almost everything under the radical sign is squared, is really asking “What would this be before it was squared?” Pull the answers out and leave the rest inside.
Simple.
This is the easiest one of all, thanks to the FTOA. Re-write the 30 as its prime decomposition to make sure there’s no perfect square hiding in there, and write out the variable in a way that will let us pull out the perfect square:
The rest of it can be left under the radical:
Word problems are what terrify most people about algebra and beyond, and I almost included a couple of them here, but I’m going to save them for a special series on how word problems are really surprisingly easy.
I hope this serves to demonstrate how knowing arithmetic really well and learning to think in terms of factors, especially prime factors, makes algebra fun and interesting, not terribly difficult.
Next post: really going to try to get to the sign rules next this time, ha ha!
















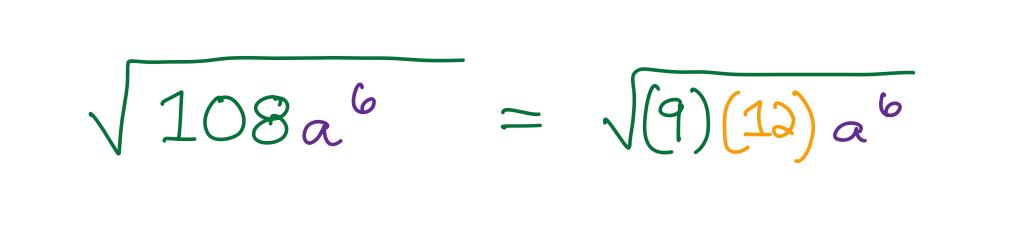



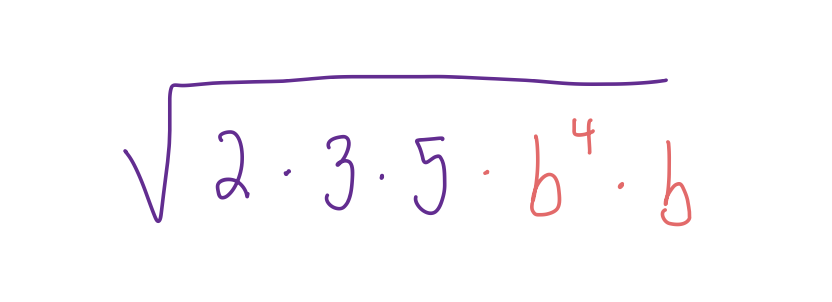

Thanks!