Elite Mathematical Training
How to Not Suck at Math, part 8
This is part of a new series about how to help yourself or your kids improve in mathematics. It’s based partly on my own experience of having to learn how to learn mathematics, partly on extensive tutoring experience, and partly on many conversations with homeschooling parents, as well as parents struggling to understand Common Core mathematics. Many future editions are already planned, but feel free to leave suggestions for future editions in the comments (open for paid subscribers) or by email to hollymathnerd at gmail dot com.
The first five posts are not behind the paywall; all future posts will be; this link will give you 10% off. If you’d like to get them but can’t afford a paid subscription, email me at hollymathnerd at gmail dot com and I’ll give you a free one.
Previous posts in the series:
Part 1: Addition and Subtraction
Part 2: Multiplication, Division, and Fractions
Part 3: The Major Key of Mathematical Fluency
Part 4: A Proof for this Approach to Numeracy
Part 5: “I’m Just Not A Math Person!”
Part 6: How the Sign Rules Work, and Why
Part 7: The Box Method of Multiplication
One way I manage wintertime depression—the kind of thing I experience when there’s so little daylight that the sun comes up an hour after I start working and has been down for an hour when I finish—is to do a lot of number theory problems. They’re fun, and challenging, and engrossing enough to get me out of my emotions.
I have long thought that number theory is something kids should be exposed to starting in middle school. My friend Gator wrote a brilliant introduction to modular arithmetic, something that typically only very advanced high schoolers in AP courses or math majors/minors ever learn, that’s accessible to middle schoolers: you can read it here.
For today’s post, I’m going to show you that number theory is both really fun and not at all beyond an average adult. Don’t worry, we’ll go slow and it’ll be fun!
Here is a problem from the book, 104 Number Theory Problems from the training of the US IMO Team. (IMO = International Mathematical Olympiad).
Sounds intimidating, doesn’t it? I promise, it’s not! You’ll understand it before I’m done.
A positive integer is written on each face of a cube. Each vertex is then assigned the product of the numbers written on the three faces intersecting the vertex. The sum of the numbers assigned to all the vertices is equal to 1001. Find the sum of the numbers written on the faces of the cube.
Whoa, sounds intense, right! It’s not, really! I’ll show you.
First, we’ll do a much simpler version of the problem.
There is a coin with two sides. Each side has an invisible number written on it. The product of the two numbers is 10. The sum of the two numbers is a 1-digit number. What is its sum?
First we’ll label the parts:
We are told that H times T = 10, and that H + T equals a one-digit number, which we are asked to find.
What two numbers multiply to get 10?
1 and 10, for sure. What else?
2 and 5.
Now we can add them up. 1 + 10 = 11, and 2 + 5 = 7. Ah, we have two possible sums, but only one fits the conditions of our problem. Our answer is 7.
That’s a very simple version of the same kind of problem, but it should give you an idea of the thought process. Now we’ll tackle the real one.
Go as slow as you need to, come back and read it again, and feel free to ask any questions in the comments.
A positive integer is written on each face of a cube. Each vertex is then assigned the product of the numbers written on the three faces intersecting the vertex. The sum of the numbers assigned to all the vertices is equal to 1001. Find the sum of the numbers written on the faces of the cube.
First, let’s draw a cube. I found one online with four sides colored and all eight vertices already labeled.
By simple inspection, we can see that the cube has six sides and eight vertexes — that’s eight corners, places where three sides of the cube touch. For example, at the vertex labeled A, the left panel (blue), bottom panel (green) and front panel (transparent) all intersect.
The problem tells us that these eight vertices are each assigned a number that’s the product (the answer in a multiplication problem) of the three faces intersecting. And if we take these eight products and add them up, the sum is 1001. We are asked to find the sum of the six numbers written on the faces of the cube.
So we need to find: the six numbers on the faces of the cube, and add them up.
Our clues are:
There are eight vertices.
There are eight products found by multiplying the three numbers that intersect each of the eight vertices.
When added up, these eight products sum to 1001.
Now we will label the eight vertices and the six faces of the cube, and make a list of where each product comes from. I’ll use purple for the top panel and pink for the front panel, which are transparent in the picture, and stay consistent to hopefully keep this easy to understand.
The six faces will be labeled:
T (bottom panel, green)
U (left panel, blue)
V (top panel, purple)
W (right panel, red)
X (back panel, yellow)
Y (front panel, pink)
and the list will show where each vertex’s product comes from.
Go slowly. Look at each vertex, at the three letters that make up the product, and the three panels those letters come from. Look at all eight of them and make sure you understand where each is coming from before going forward.
Now we’re ready to start doing math!
We know that the eight products add up to 1001. That means we have this equation:
YUT + UTX + XTW + YTW + UVY + XUV + VXW + WVY = 1001.
This is a complicated mess, so we’ll do some factoring.
You already know how to factor, even if you don’t think you do.
How many nickels are worth a quarter?
You just said “5” in your head without thinking for more than a few seconds. You know that a nickel is worth 5 cents and a quarter is worth 25 cents, and even if you weren’t aware of doing it, you realized that 25 = 5 x 5.
5 instances of 5 cents = 25 cents.
Imagine you were adding up the value of three piles of coins and were given this problem, where each part of the formula is a pile of coins and Q is how many quarters.
7Q
3Q
10Q
Your problem is:
7Q + 3Q + 10Q = How much money?
You would add 7 + 3 + 10 = 20 quarters, then multiply 20 times 25 cents to get $5, right?
You just factored out the Q. What you did was this:
Q(7+3+10) = Q(20)= 25 cents(20) = 500 cents = $5.
You just did it in your head, or perhaps on your fingers or calculator.
Just like you factored out the Q to add up the money in three piles, we will factor this equation to make it easier to handle.
So now we know that we have three numbers, which multiply together to get 1,001. Three factors of 1,001. And we know that those three numbers each can be split into two parts (x and y; v and t; w and u), which gives us the six numbers of our six cube faces.
Let’s find three factors of 1,001. If we’re lucky, there will be ONLY three factors and we won’t have to try to break it down farther, the way we did with our simple coin question that had two possible answers.
To find factors, there are lots of methods. I like using the divisibility rules. For something to be divisible by 2 or 4, it has to be even. That feels intuitive, I bet. So probably is that if a number is divisible by 5, it ends in 5 or 0. (5, 10, 15, 20, 25, 30….). To be divisible by 6, a number has to be divisible by 2 and 3 both, which is a little less intuitive (but I’ll write a post on it eventually).
The two rules that are most helpful are usually the rules for 3 and 9. If a number is divisible by 3, its digits add up to something divisible by 3. Likewise for 9.
(Again, I’ll write a post on this eventually, but this one is long enough.)
1,001 has a digit sum of 1 + 0 + 0 + 1 = 2, which isn’t divisible by 3 or 9.
So we’ll start at 7:
There you go! You just understood a number theory problem used to train the US International Mathematical Olympiad team.
Go you!!













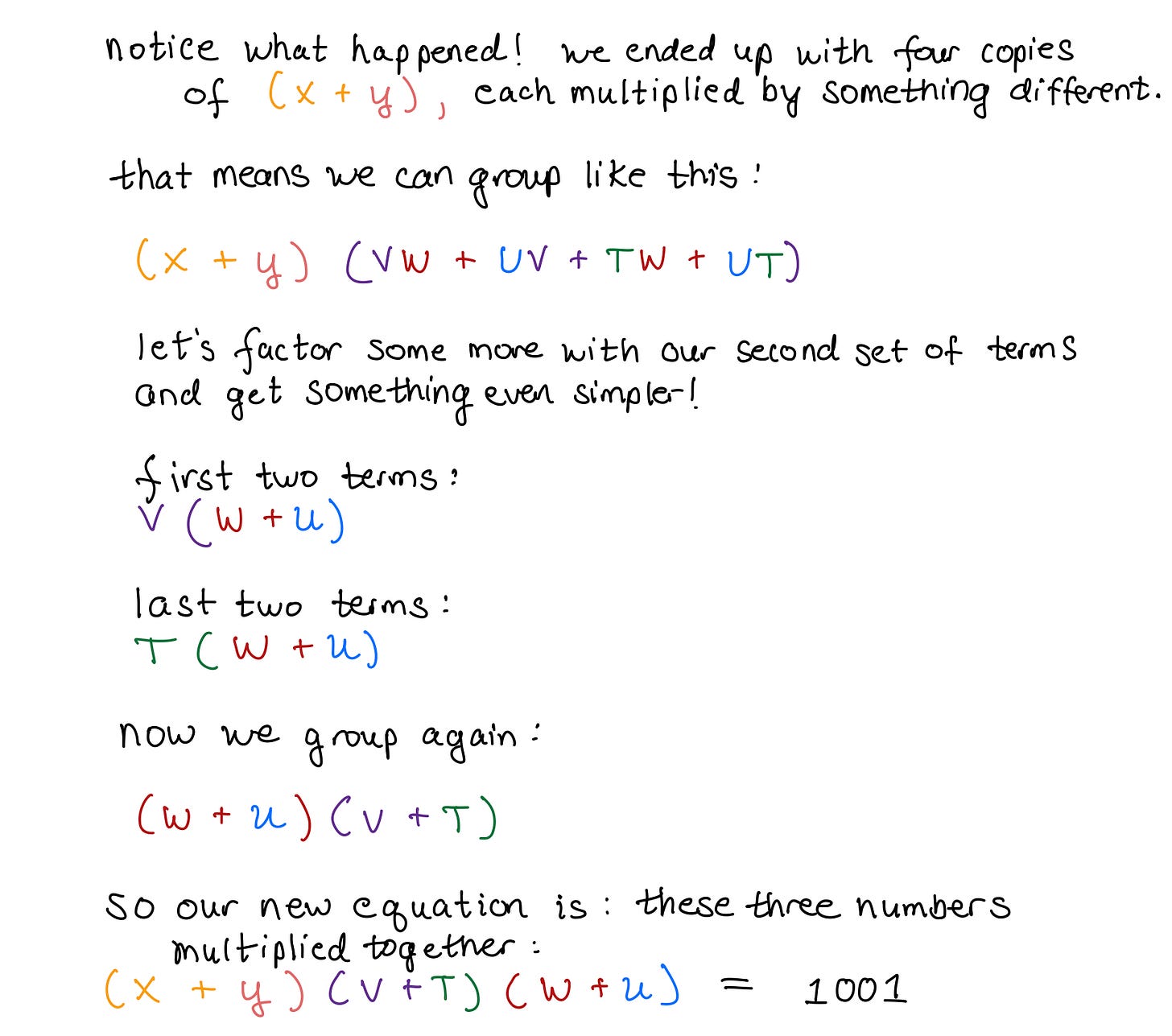
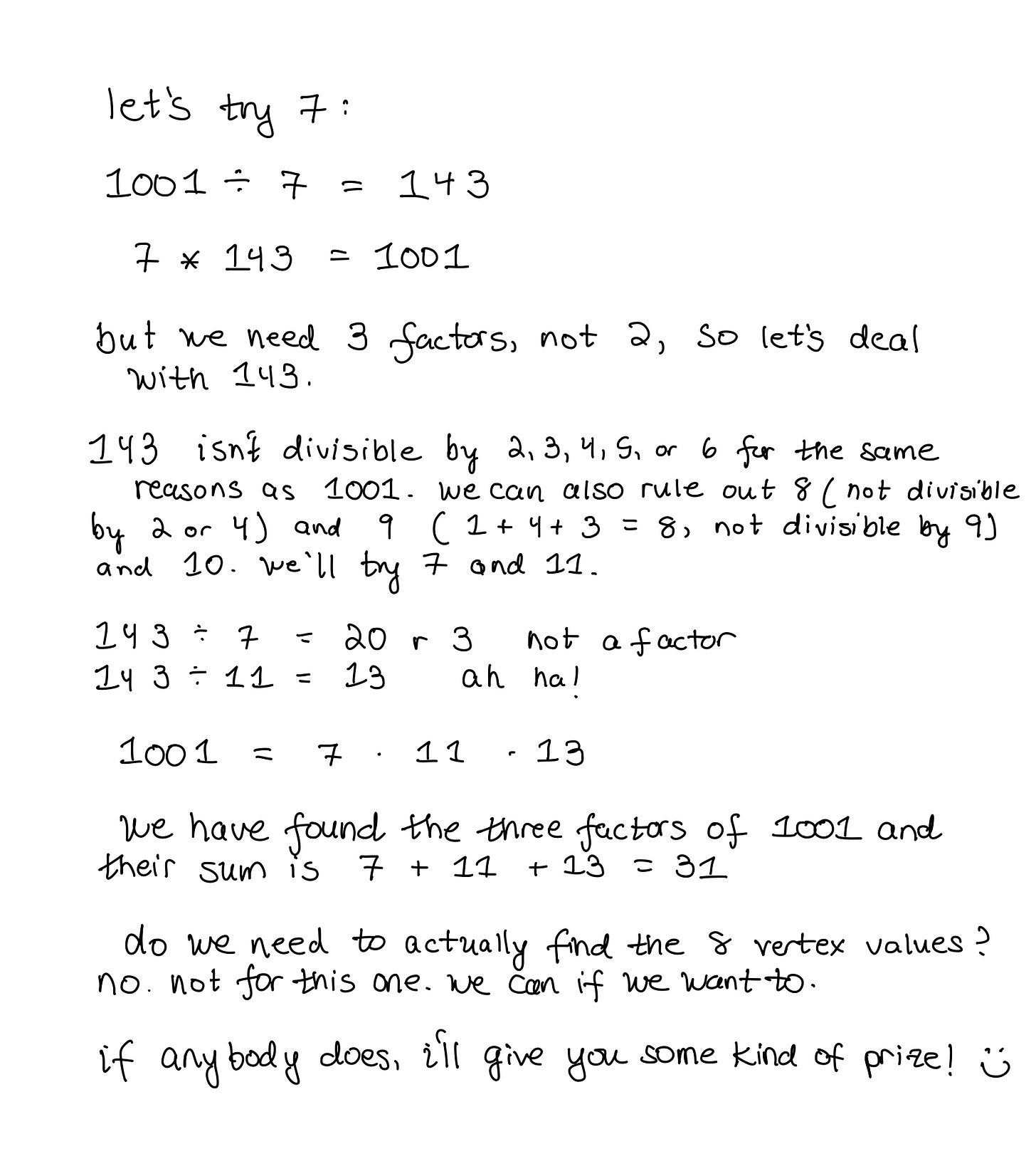
Hello Holly and thank you so much for this series. I found the eight values, but it doesn’t matter their order right? At least they all add up to 1001. However, in factoring, I came up with four copies of T and V and two copies each of YU, UX, XW AND WY. I don’t recall ever learning this kind of math before, or maybe I just glazed over when it was taught in school. Your explanations make lots of sense to me and even though I’m slow, I can follow along. It took me most of the morning and some afternoon to work through it while referencing your figures. The eight values I came up with are: 140, 120, 12, 14, 350, 300, 30 and 35. I’m not looking for a prize, just knowing that I solved the problem correctly is prize enough for me😀
I think this is the kind of thing I could probably Google and get an answer but...could you describe in 100 words or so what "number theory" is? I'm asking because like a lifetime ago (actually the divorce was only finalized 10 years ago but I may be experiencing some weird emotional red/blue shift because I want it to be in the distant past) I was married to a guy who minored in mathematics as an undergraduate and he was incredibly dismissive of people who in his words confused "arithmetic" with "mathematics." And in his view, calculus and statistics was "arithmetic." Mathematics, apparently, was restricted to the kind of arguments that might have been put forth by an intellect like Srinivasa Ramanujan.
Your post was very cool and it got me thinking along some lines I had not previously thought about, but it's also the kind of reasoning my arrogant ex would have dismissed as "arithmetic" -- solving a problem through clever but ultimately iterative, exploratory, "find the number that fits" methods -- not a universal abstract solution expressed in the language Bertrand Russell would have used.
I'm really asking you to provide one more reason I should stop feeling inferior to a person who left my life a decade ago; if that's not your jam I perfectly understand. I really am interested in a Richard Feynman "explain it to a five year old" definition of number theory, though.