Important Note: for those of you who don’t code, the use of an exclamation point next to an equals sign (!=) means “does not equal”.
Examples: (2 + 2 = 4) and (2 + 2 != 5) and (2 + 2 != anything else).
Comments will be open for paid subs after I finish work on Friday, November 15, and will stay on over the weekend. Restack-with-note is available for those of you on Substack Notes who just can’t wait.
This post is about the latest battle of the 2 + 2 != 4 war.
A reader who knows that he doesn’t know much about mathematics sent me the latest Twitter battle in this war and asked me to comment. I am happy to do so, for his sake, but I am also furious that this is happening again.
Why am I angry?
The Power of Mathematical Excellence
I am writing by typing on an ergonomic keyboard while walking on an under-the desk treadmill at a standing desk. None of those are cheap.
I am writing after having cooked an expensive dinner ordered from one of the meal delivery services.
My post-writing plans include going to my easel to play around with professional-grade charcoal drawing pencils on professional-quality drawing paper, and visiting Etsy for more Christmas shopping.
I still wear my beloved Chuck Taylors, but now I pay $25 more than it would cost to get them locally. I spoil myself by ordering them online from Etsy sellers who embroider them with lovely designs.
This morning, I spared my bad shoulder from several days of pain by hiring someone to deep-clean my bathtub.
I’m not rich, by any means.
These are fairly modest as non-essential expenditures go, but my life is luxurious far beyond anything I ever dreamed I could have as a kid. And well beyond what my past would predict.
I grew up in a trailer park.
My mouth is a mess because I got very poor dental care in early childhood.
One of my earliest childhood memories occurred in the lobby of a payday loan place.
I was sixteen years old the first time I knew why there are sometimes two forks on a dinner table.
Nothing in my background suggests that I should be anywhere near as comfortably middle class as I am now.
I got to become a class-climber1 for one reason, and one reason only: I got pretty good at mathematics.
Mathematical excellence is a game-changer for career prospects. And that makes anything that keeps kids from pursuing mathematical excellence—any obstacles to their ability to conceptualize mathematics as a reliable, dependable field of human endeavor that has unchanging, learnable rules—a threat to their futures.
Anyone who presented such a thing to kids on purpose and with conscious intention would, in my opinion, be committing a type of child abuse.
And that’s what a group of our public intellectuals are doing.
What Mathematics Is
Mathematics is the abstract science of number, quantity, structure, space, and change. What does abstract mean? It means that concepts—like two, addition, seven, subtraction, prime, composite, nineteen, etc.—are ideas that don’t rely on physical objects to exist or to be understood. Instead, they represent universal principles or properties that can apply in many situations, regardless of specific examples.
In mathematics, abstract concepts allow us to think about numbers, operations, and relationships without needing a concrete representation. For instance, "two" can refer to two apples, two cars, or any other pair, while still representing a universal quantity. Similarly, "addition" applies universally, whether we are adding amounts, objects, or any set of entities that can be combined.
Mathematics involves the study and formulation of patterns, relationships, and logical structures, allowing for the exploration of concepts through pure reasoning, calculation, and rigorously defined symbols and rules. The foundation of logic permits humans to trust mathematics and build civilizations on it — roads and bridges, but also modern communications, medicine, and financial systems.
Mathematics Alone Provides Certainty
I once had an argument with a friend about whether mathematics is the ultimate source of certainty.
My position was, and is, that mathematics alone provides certainty. He argued that other things can provide just as much certainty.
His example was fire: that if I were set on fire, I would have as much certainty as I do about a proof.
I understood what he was thinking, and why, but he was wrong.
When I have a nightmare about being burned alive, I am absolutely certain that I am experiencing being set on fire. But I’m not.
I wake up and don’t even smell like smoke.
An Example of Mathematical Certainty
Prime numbers are those that are only evenly divisible by 1 and themselves.
7 is prime because dividing it by any number other than 1 or 7 leaves a remainder.
10 is not prime because you can divide it by 2 or 5, as well as 1 or itself, and have no remainder.
Cousin primes are pairs of prime numbers that differ by exactly 4. 13 and 17, 19 and 23, 37 and 41 — those are all examples of cousin primes.
I will prove to you, with absolute certainty, that there is one, and only one, prime number with two cousins: seven.
7 has as its cousin primes the prime number 3 (7-4) and the prime number 11 (7+4).
No other prime has two cousins, and you can count on this more fully than you can count on the idea that you’re breathing, you’re not on fire, or that you know the weather outside.
Here is how you can know this.
Any prime number p with two cousins must be in a sequence like this:
p-4, p, p+4, where all three are themselves prime.
You can see how it works for p = 7.
p-4 = 3, which is prime.
p = 7, which is prime.
p+4 = 11, which is prime.
Consider that every third whole number is evenly divisible by three. That’s how “three” works.
Count for awhile: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Every third whole number is evenly divisible by 3.
3, 6, 9, 12.
The other numbers either leave a remainder of 1 when you divide by three: 1, 4, 7, 10; or a remainder of 2 when you divide by three: 2, 5, 8, 11.
There are no other possibilities.
Keeping that fact in mind, consider the possibility of a sequence other than 3, 7, 11 that are cousin primes.
Those would be p-4, p, and p+4, and all three must be prime.
p-4 could not be divisible by 3, since we are considering the possibility that it’s not the 3, 7, 11 sequence and if it is divisible by 3, then p-4 isn’t prime.
That means that p-4 must have either a remainder of 1 or 2 when divided by 3, as there are no other possibilities.
If p-4 has a remainder of 1 when divided by 3, then p-4 = 3x + 1 for some whole number value of x.
Just make sure that’s clear, I’ll use the examples from before.
4 has a remainder of 1 when divided by 3, and 4 = 3x+1 for x = 1.
7 has a remainder of 1 when divided by 3, and 7 = 3x+1 for x = 2.
Likewise, if p-4 has a remainder of 2 when divided by 3, then p-4 = 3x + 2 for some whole number value of x.
5 has a remainder of 2 when divided by 3 and 5 = 3x + 2 for x = 1.
8 has a remainder of 2 when divided by 3 and 8 = 3x + 2 for x = 2.
See how that works?
Remembering that our sequence is p-4, p, p+4, and that p-4 has to equal 3x + 1 or 3x + 2, one or the other (again, since it’s not 3 and, being prime, is not divisible by 3), we have an easy solution.
If p-4 = 3x+2, then p = 3x+6. (Just add four to each side of the equation.) And 3x + 6 is divisible by 3 for any whole number value of x, so then p couldn’t be prime.
If p-4 = 3x+1, then p + 4 = 3x + 9. (Just add eight to each side of the equation.) And 3x + 9 is divisible by 3 for any whole number value of x, so then p+4 couldn’t be prime.
For any p-4, p, p+4, at least one of them is always, always, always divisible by 3.
Therefore the one and only sequence of three cousin primes in a row—and therefore the one in the middle having two cousin primes—is the one that includes three: 3, 7, 11.
Seven is the only prime with two cousins, and you can count on that never-changing, perfectly certain fact.
Where else in life can you get total certainty?
Mathematics is dependable, reliable, and solid.
Causing humans (especially kids, the population most likely to be learning about 2 + 2 = 4) to doubt that mathematics is all of these things is morally repugnant.
The Bullshit Claims: Case 1
Now, I’m going to explain the things my emailer asked me to explain: the examples he was seeing cited on Twitter but he didn’t understand.
The first one is this: that 2 + 2 = 11 in base 3.
Our number system is base 10. That’s why our numbers work the way they do. Take the number 7,777:
Base 3 works the same way, only with 3 instead of 10. Let’s convert a base 10 number, like 17, to base 3 to see how it works.
17 is one of my favorite primes, so we’ll use that. To convert to base 3, repeated division by 3 and recording the remainders is the most reliable method:
Here’s how you can see that this is 17 in base 10:
Now that we understand how base 3 works, here’s why the “gotcha” of saying that 2 + 2 = 11 in base 3 just demonstrates that some people are willing to lie to you about easily proven mathematical facts:
Two plus two is four. Period. Even if you write it in another base because you think you’re clever.
That is what four means: the thing you get by adding two and two.
This claim about base three is as absurd as saying, ‘Two plus two isn’t four! It’s cuatro!’” and then honestly believing that you’ve made a valid point, as if “cuatro” isn’t literally just another way of saying four.
The Bullshit Claims: Case 2
The other example that gets used a lot involves rounding. Depending on how precise you need to be (guesstimating next year’s federal budget vs dosing the insulin for a diabetic toddler) the way people choose to use rounding is different for different scenarios.
Some people like the rule of rounding up if you get .5 or above and rounding down if you get .4 or below. So those people say:
2.4 + 2.4 = 4.8, which rounds to 5, therefore 2 + 2 = 5.
This is horseshit and plays a trick in plain sight. If you’re rounding, then round. 2.4 would round down to 2, so you’d be doing 2 + 2, not 2.4 + 2.4. And 2 + 2 = 4.
The Bullshit Claims: Case 3
Another common claim that these people make involves the use of modular arithmetic.
Modular arithmetic is a skill that anyone can learn. Here’s an explanation that should be accessible to most middle schoolers, by the great
, whose Substack you should subscribe to.To give a simple example, think about even and odd numbers. Even numbers are divisible by 2, meaning they have no remainder when divided by 2. Odd numbers, on the other hand, always leave a remainder of 1 when divided by 2.
Modular arithmetic focuses on these kinds of remainders from division. In code, if you needed to check for even numbers only, you would write:
x if x % 2 == 0This means, “check x only if, when you divide x by 2, there’s no remainder”—which confirms that x is even.
To check for odd numbers, you would write:
x if x % 2 == 1This means, “check x only if, when you divide x by 2, the remainder is exactly 1”—ensuring that x is odd.
Modular arithmetic has many practical applications in coding, especially when working with large numbers. However, people who try to tell you that “2 + 2 != 4” because of modular arithmetic are lying to you.
Just like in our regular base-10 system, where we have only ten digits (0–9) and then start again with 10, in modular arithmetic, numbers "wrap around" after reaching the modulus. For example, in mod 3, the only possible results are 0, 1, and 2, since these are the only possible remainders when dividing by 3.
When someone says “2 + 2 = 1 in mod 3,” here’s what it means.
First, they’re using incorrect notation. Modular arithmetic uses three lines, not two as in the normal equals sign, and the word is not “equals.” It is “congruent to.” So it is properly written like this:
And the above is pronounced, “Two plus two is congruent to one, mod three.”
What does that mean?
2 + 2 = 4, and 4 divided by 3 has a remainder of 1.
In other words, the only reason that:
is literally because 2 + 2 = 4. If 2 + 2 != 4, then in mod 3, 2 + 2 would not be congruent to 1.
The Bullshit Claims: Case 4
The remainder of the claims that my emailer sent me were from a Twitter thread.
In it, the author makes points of ridiculous pedantry. They’re the kind of thing that I would’ve come up with when I was an angry, traumatized nine-year-old who just wanted to force the adults to listen to me talk.
It’s the kind of thing that extremely annoying children often come up with.
“1 foot plus 1 foot equals my two feet and I’m 1 person so 1 + 1 = 1, ha ha!”
“1 sock plus 1 sock equals 1 pair, so 1 + 1 = 1, ha ha!”
“50 states equals 1 country so 50 = 1, ha ha!”
In other words, he swaps units repeatedly and thinks he’s clever.
If a child I was babysitting tried this, we’d have a gentle conversation about why using your own special definitions in place of definitions that are commonly agreed upon by everyone is a type of immature self-centeredness, and is a terrible, unkind way to treat other people—a way that won’t help them make friends or have a good life.
If that didn’t work, I would turn the tables on them. “I said you could stay up until 9pm if you read two chapters of your book. You read chapter 3, which is one chapter, and chapter 4, which is one chapter, but 1 + 1 = 1, like you said, so you have to go to bed at 8pm like usual, ha ha!”
The author attempts to make a political point partway through the thread, and I at least salute his honesty there. That particular point can only be made by people who try to force total re-definitions on the rest of us, without proper consideration for the ways that re-definition changes everything else and without our consent.
Here are screenshots of the whole thing:
The author got community noted, and he insists that the community note makes his point — and yet he used this to repeatedly double down.
His point is apparently that he’s entitled to make his own definitions up for everything, including mathematics itself, and if the rest of us don’t accept his definitions, we’re wrong:
The tweet he quoted:
I want very badly to believe that this whole thing was just a bid for engagement, perhaps to get on the Twitter payout system, but it just isn’t.
He honestly thinks that he has some deep understanding of mathematical complexity.
Why This Twitter Thread Is Evil
Mathematics is a game-changer for career and economic possibilities.
Mathematics is accessible by anyone willing to work hard enough to master it, and nobody needs mathematical excellence more than members of the groups we call “underprivileged” or “marginalized.”
Little kids growing up in poverty, as I did, a disproportionate number of whom are black, should be getting all kinds of encouragement to get good at mathematics. They should be presented mathematics with wonder, awe, and the entirely true promise that these rules are solid, dependable, and trustworthy.
That unlike science, which is never fully certain, or history, for which the victors write the books and so another perspective is always worth considering; mathematics presents a path to immutable, unchanging, pure, and rock-solid truth.
Instead, it’s apparently the top priority of not one but two black Harvard-associated academics—and quite a lot of leftie/progressive types on Twitter—to make damn sure that little kids think math isn’t just challenging, it’s challenging in an insurmountable way.
You can’t learn and master the rules.
The rules change all the time!
It tells children that math is whatever an authority says it is—and that they’re ‘wrong’ if they don’t agree, even if the authority is just making shit up.
It’s disgusting. And it hurts most the group of little kids who, in our identity-obsessed culture, are the most likely to be given these men as examples of role models to look up to.
Why Do People Keep Doing This?
I can give you three hypotheses and four possibilities.
One, mathematics is often the first and only subject a kid finds challenging. Abstraction is a skill that has to be developed. The rules don’t change. There are definite right and wrong answers. If you add 2 + 2 and you get anything else but 4, you’re wrong. It doesn’t matter why you think your answer is right, you’re wrong. This is something that a kid who’s always done well in other subjects can find overwhelming, since persistence and dealing with challenges are not skills they’ve had to develop yet. So they either invent a narrative that their innumeracy is indicative of virtue — my undying respect to
for elucidating this better than anyone ever has, to my knowledge, in this post — or they find a way to re-define math for themselves as something whose rules are in flux and re-definable by them, as the Twitter thread author did. This is often the path taken by people who are smart but lazy and/or afraid of failure.Two, they have a political motive, often related to the issue the author brought up in tweets 13 through 16.
Three, they’re dumb.
Each hypothesis represents a possibility. A fourth possibility: some combination of two and three.
As to which one applies to the author of the twitter thread, the proof is left to the reader.2
This is an inside mathematical reference. In mathematics, “the proof is left to the reader” is a phrase often used in textbooks or lectures when a proof is straightforward enough for a knowledgeable reader to figure out on their own. It’s a subtle challenge, suggesting that while the statement is true, the reader’s own effort will deepen their understanding. Here, it suggests that the reader can judge the author’s arguments for themselves, using logic and reasoning, as they would in mathematics.






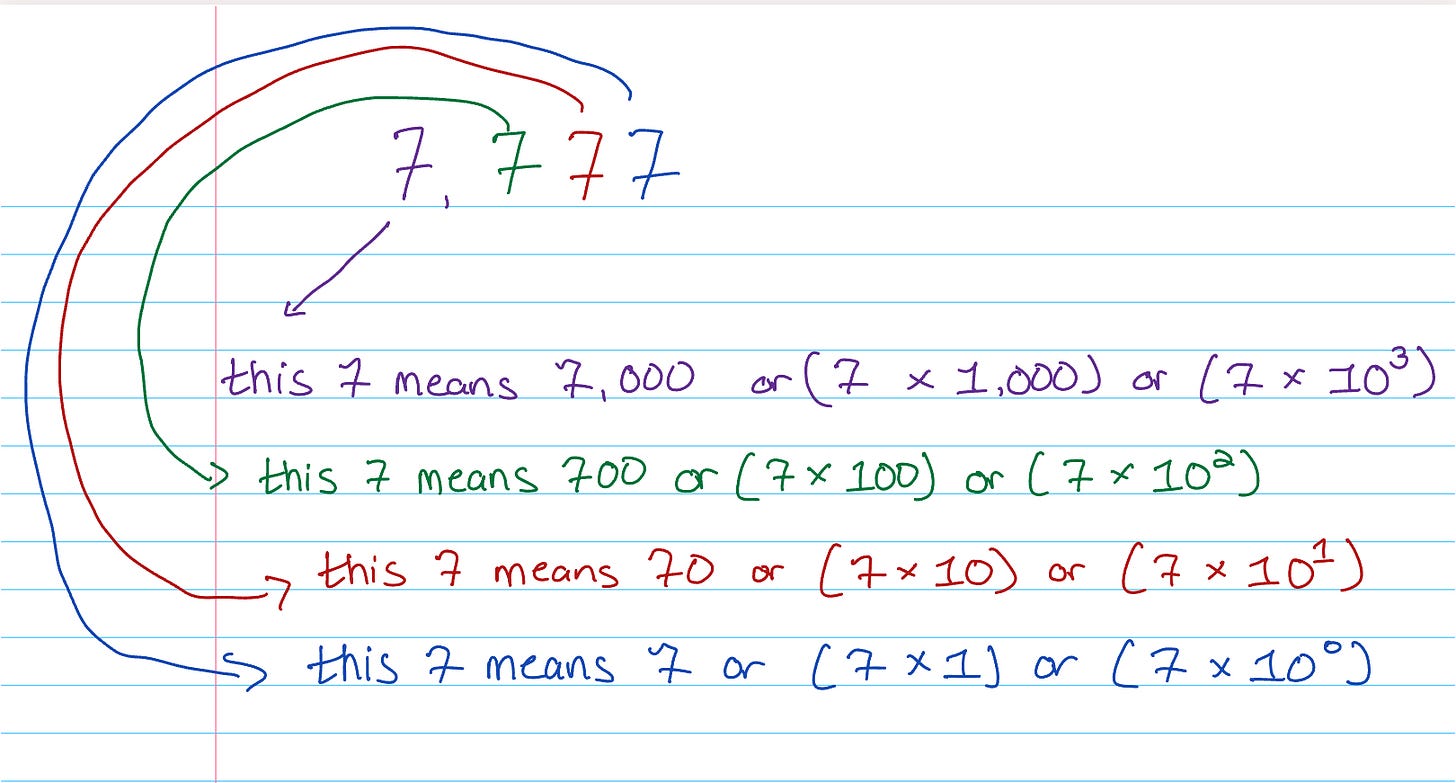



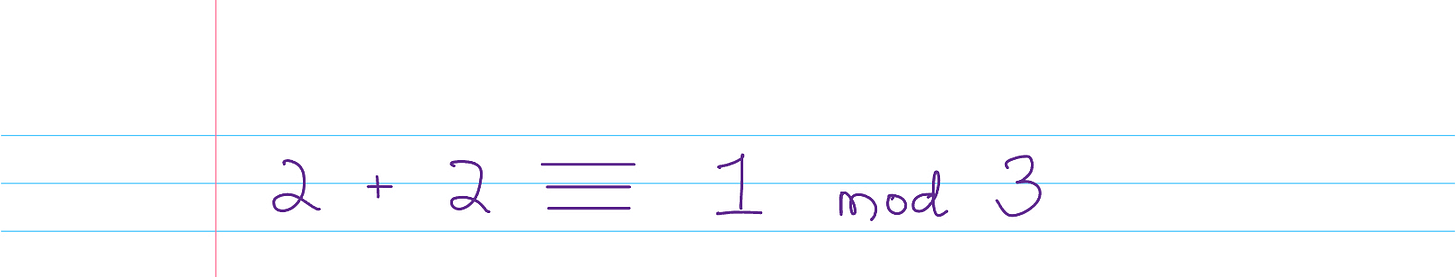






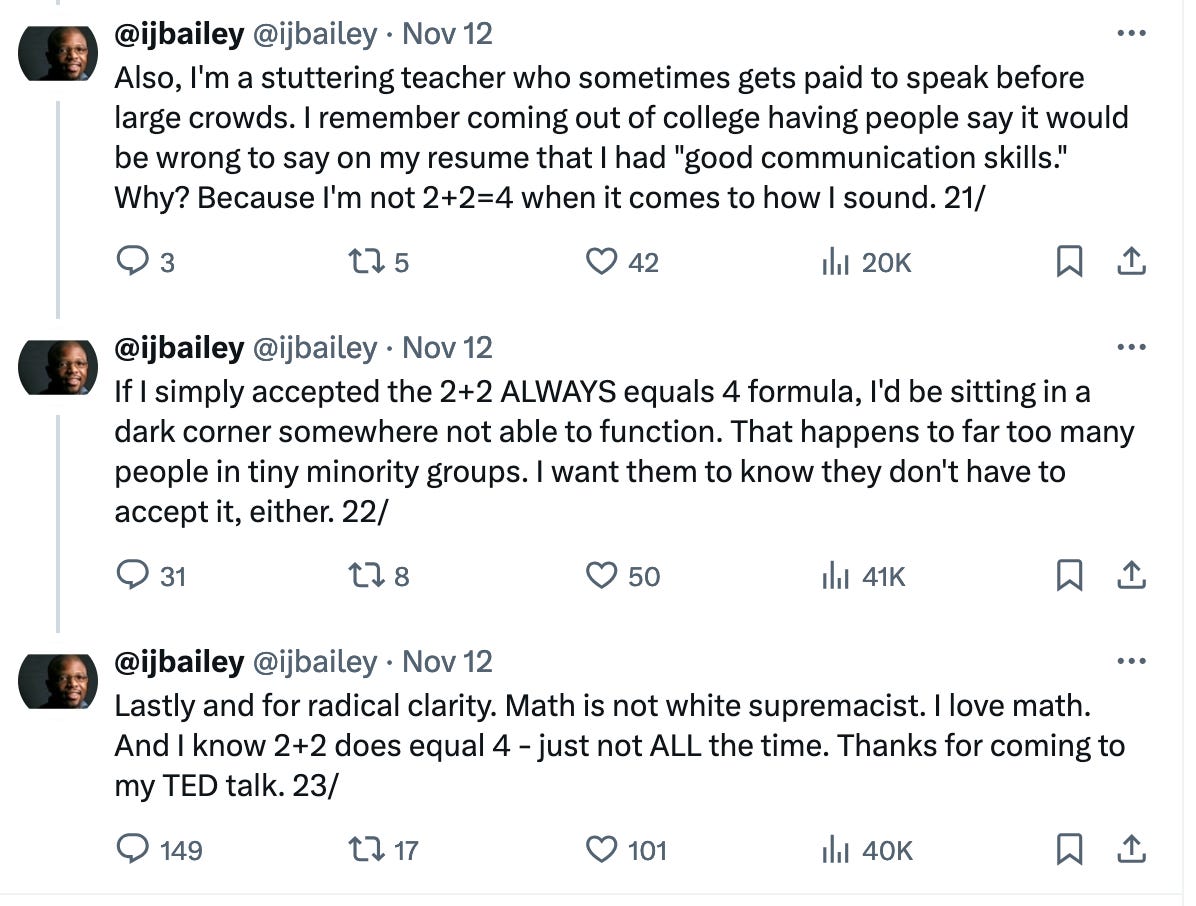




That Twitter thread is infuriating. I think there’s no question that at least hypothesis #2 applies in this case. Here’s what I think the author is hoping: Most people are not particularly well educated in science, sadly. But even they generally recognize that math lends itself to more certainty than biology. (As a biologist by training myself, I’ll be the first to recognize that my field is “squishier” than the “harder” sciences.) So, by casting doubt on something that even non-scientists think they know for sure (2+2=4) in a field like math that is known for its absolute truths, posters/activists further open the window to sowing doubt regarding things people thought they knew for sure (there are two sexes, and individual mammals can’t switch from one to the other) in a field they know is less prone to absolutes.
I came across the Twitter thread on my feed and wondered how people have so much time between their moral outrage addiction about the world, rage posting, and important performative activism to break math rules and tweet nonsense thread about it. Kudos for your patients and methodical takedown of alternate/dissociated reality maths.