This post has a ton of pictures and is also longer than most email clients can handle, so you may want to read it at the Substack website by clicking on the title above.
NOTE: A few people are having issues reading on a phone, but when they look on a computer it looks right. Substack appears to have issues with LaTeX (the mathematical typesetting) on the phone interface, specifically with dropping plus signs (so what should be 5+1 looks like 51 instead), so read on a desktop or laptop if you can. I have reported it to Substack but it’s unlikely that they’ll actually do anything. Sorry; it’s beyond my control.
Edition 3 of Monday Morning Love
This is my series for starting each week of on a note of positivity! I write about something I love and publish it first thing Monday Morning, in an attempt to start the week off on a positive note.
I’m not going to put these behind the paywall, but if it motivates anyone to become a paid subscriber, my student loan balance would appreciate dwindling a bit in your honor, and there’s a special deal at this link. Comments are open for paid subscribers. Feel free to weigh in on what’s most interesting to you out of the topics I’m thinking about right now, as things I love and that it might be fun to write about—the novel A Widow for One Year, by John Irving; riding a bicycle; coding; Halloween; learning to draw in colored pencils after having gotten to a reasonably high skill level in graphite; the novel The Poisonwood Bible, by Barbara Kingsolver; learning to paint; finding unobtrusive ways to get more exercise in my day.
Edition 3: I love Number Theory
I promise that this is going to be understandable and accessible, so I hope those of you who are terrified of math will keep reading. I will answer questions in the comments if I can—Monday is a workday so I will be a bit busy but should still have some time.
And for the math lovers, there’s a Putnam practice problem at the very end of the post. Feel free to do your own proof and post it in the comments or on Notes.
Number Theory is a branch of mathematics that deals with the properties and relationships of numbers, particularly whole numbers. It's like a study of the building blocks of math.
Number theory problems are enormously fun for many reasons, among them that some of the fun, fanciful aspects of philosophy and other arguments come into play, like thought experiments. But because number theory solutions rely on logic and mathematics, it’s possible to settle these issues with certainty and arrive at firm, unchanging conclusions, which is, to me anyway, enormously comforting and satisfying.
A number theory solution is called a “proof,” because that’s what it provides: proof.
One of the most famous number theory proofs is the one that tells us about prime numbers, and that they are infinite. We can never run out of them.
Reminder: a prime number is one that is only divisible by 1 and itself. The only even prime is 2, since all the larger even numbers are divisible by 2. Here’s a chart with the prime numbers under 100 shaded in purple.
Why Prime Numbers Matter
Prime numbers are the building blocks of arithmetic, which is why the most fundamental fact of arithmetic is called the Fundamental Theorem of Arithmetic. I explain it, and why it matters, in great detail in part three of my series, How to Not Suck at Math (the first five posts are free, the rest for paid subscribers).
Here’s a shorter explanation: every integer greater than 1 can be written as the product (the answer in a multiplication problem) of a unique combination of prime factors. (The uniqueness goes up to the order, meaning that 2 x 5 and 5 x 2 are not considered different combinations since they have the same parts, just in a different order.) This combination is called a prime decomposition.
Example: think of the number 12. 12 is composite (not prime). If you know your times tables, you know that you can get 12 via multiplication a couple of different ways. 2 x 6 and 3 x 4 probably come to mind. 6 and 4 are not prime and can be broken down into prime factors of their own, so both possibilities end up in the same place.
This will always be the case. Every integer greater than 1 will break down into prime factors and have a unique prime decomposition.
Another example, 360, has many possible combinations. 2 x 180, 3 x 120, 4 x 90, 5 x 72, 6 x 60, 8 x 45, 9 x 40, 10 x 36, 12 x 30, 15 x 24, and 18 x 20. I won’t write all of them out, but here are a few to show that they all lead to the same prime decomposition of 2 x 2 x 2 x 3 x 3 x 5.
The fundamental theorem of arithmetic teaches us that it will always be this way — when we take any integer and break it down into factors, those factors will always keep breaking down until we end up with the same set of unique primes that multiply into the original number we’re working with.
Here is something I coded. It’ll be wonky on a phone, so look at it on a tablet, desktop, or laptop. It will let you test any number to see if it’s prime and also will give you the prime decomposition of any number.
The Beauty of Infinite Primes
I’m going to try to make it easy to understand the beauty of the original proof, the one Euclid came up with about 300 years BC, by giving you a small version of it.
Let’s pretend that I am convinced we only have a few primes. I have convinced myself that the only prime numbers are these: {2, 3, 5, 7, 11, 13, 17}.
How might you prove to me that I’m wrong?
Here’s one way. You might say:
“OK, cool. Let’s try this. First multiply those primes together. What do you get?”
I do the multiplication and get 510,510. You say:
“Awesome. I get that, too, so we both did the multiplication right. Now let’s add 1. What does that give us? 510,511, right?”
I nod. You say:
“Now, it’s a fact that 510,511 is either prime or composite. Correct?”
I nod again. Then I say, “I remind you that, according to my beliefs, it has to be composite, because it’s not in my defined list of the only primes.”
“Ah ha!” you reply. “But we have a problem. If we divide 510,511 by any of your list of the only primes, it won’t divide evenly, will it?”
I think about this and admit, “No, it won’t. That’s how multiplication and division work. Just like if we multiply 2 times 5 we get 10 and add 1, we get 11, but 11 divided by either 2 or 5 won’t divide evenly — it’ll have a remainder of 1 — you’re right. Dividing 510,511 by any of the primes on my list it will have a remainder of 1.”
You elucidate what this means: “So none of those primes are a factor of 510,511. Which means that either your list doesn’t have all the primes or that 510,511 is itself prime. Either way, we have more primes than what’s in your list!”
That’s the fastest way to proving me wrong, a better method than simply finding another prime — since if you did that, I might just add to it my list and say, “Now we have a complete list and these are the only primes.”
This method, if you think about it, shows both that those aren’t the only primes and that there are infinite primes.
That’s why I gave you this small version, because the big version is essentially how Euclid proved infinite primes, only he did it more abstractly. By not using specific numbers with a specific answer to the (multiplication + 1) thought experiment, it’s a little harder for a non-math person to grasp, but this is the same method. This is what Euclid used to prove infinite primes in 300 BC.
There are many thousands of other number theory problems, and each allows us to solve a puzzle and prove something beyond all possibility of doubt.
Number theory problems make me so happy that I have to discipline myself never to start one after about 7pm. If I do, it’s fairly likely that I end up working when I should be sleeping, often all night.
The Importance of Prime Numbers
Prime numbers play a crucial role in cybersecurity, because they are used in creating secure ways to protect information online. They help make codes that are easy to create but extremely hard to break. This ensures that our online communications, financial transactions, and personal data stay private and safe from hackers.
As the fundamental theorem of arithmetic shows, they are the building blocks of mathematical understanding. So I’m going to give you one more example of a number theory problem and its solution, focusing on primes. This will be something useful if you’re just thinking about math for fun, or either studying math yourself or homeschooling a kid. It will also use what we’ve just learned about the fundamental theorem of arithmetic too, which will be very satisfying, so I hope at least a few of you are still reading!
See that weird three-lined symbol where you might be expecting an equals sign? That’s not an error. I’ll write a post on modular arithmetic someday, but for now all you need to know is that it means “this is what the remainder is if you divide by the mod”. So the whole problem reads: “show that if you take the square of any prime larger than 3 and divide it by 24, it will always have a remainder of 1.”
For example: 5 is the first prime larger than 3. 5 squared (5 x 5) is 25. 25 divided by 24 is 1 with a remainder of 1. The next largest prime is 7. 7 squared is 49. 49 divided by 24 is 2 with a remainder of 1. Dividing by 24 will have a remainder of 1, always—this is always true, of the square of all primes greater than 3. Literally every single time!
The fun in this problem is figuring out why it’s true and writing an airtight argument. Let’s do it!
The first thing we know for sure is that every prime larger than 3 is odd. We know this because every even number is divisible by 2, so 2 is the only even number that’s prime. 4 isn’t prime because it’s divisible by 2, not just 1 and itself. Same with 6, 8, 10, 12, and so on.
Now, remember the examples of 5 and 7, both of which have a remainder of 1 if we square them and divide them by 24. We can make it a little simpler by just subtracting 1 from the squares at the start:
So now we see that our problem, showing that any prime greater than 3, when squared, has a remainder of 1 when divided by 24, is the same thing as:
Now we can use the fundamental theorem of arithmetic!
If we know the prime factors of 24, we know what this expression has to be evenly divisible by.
So we know that:
We can factor the problem pretty easily because 1 is itself a square (1 x 1 = 1). Why does that matter?
It is a known pattern in mathematics that the difference of squares (a square minus a square) factors the same way every time. Here it is in algebra, and then a few concrete examples:
Hopefully the concrete examples help show that it’s true. 25 - 1 does equal 6 x 4, and 49 - 1 does equal 8 x 6. The pattern here, one square minus another square, always works, and 1 being its own square lets us factor our problem like this:
So to solve this problem we have to show that for every squared prime, p greater than 3, the combination of p+1 and p-1 give us a factor of 3 and a factor of 8 (because three instances of 2 equals 8, and because 2 x 2 x 2 is the other part of 24’s prime decomposition).
Remember: just because we know that:
doesn’t mean that we can assume anything about what numbers might or might not have a factor of 24 (and therefore of 3 and 8, or 2 x 2 x 2).
We know that anything with a factor of 24 also has factors of 3 and 8, but that’s all we know for sure at this point!
We are trying to prove that, for primes greater than 3:
The 3 part is easy! Notice that p-1, p, and p+1 are three consecutive integers. One less than the prime, the prime, and one more than the prime.
Well, out of every three consecutive integers, one is divisible by 3, always. That’s what counting by 3s is — counting by the numbers divisible by 3. You are counting numbers divisible by 3 when you count by 3s and count 3, 6, 9, 12, 15, and so on.
So the 3 is easy. Now we just have to show that there are at least 3 instances of 2, to get us up to our factor of 8 — which is 2 to the 3rd power (2 x 2 x 2), remember — that, along with 3, makes up the prime decomposition of 24:
How can we do this?
Every odd number can be represented as 2n+1 for some value of n. A few examples, using the numbers 5 and 7 as well as 25 and 49, the squares of 5 and 7 that we’ve been working with already:
5 = 2n+1 for n with a value of 2.
25 = 2n+1 for n with a value of 12.
7 = 2n+1 for n with a value of 3.
49 = 2n+1 for n with a value of 24.
Let’s square 2n+1 and see what we get:
We can show that the square of every prime greater than 3, minus 1, has a factor of 8 by showing something about all odd numbers, since every prime greater than 3 is odd anyway. This is a way of tackling the problem that uses a known finding of number theory, which is why I knew to jump right to it.
How might you get there if you’re new to number theory? Number theory is all about finding mathematical patterns, so one way to figure out the direction to go with a problem is to make a list of numbers that fit patterns and see what jumps out at you. For this one, you might make a chart like this:
When you study this chart, you might see that every squared prime minus 1 has at least an eight (a factor of 2 to the third power at a minimum) or a factor of 3. You might keep playing with a chart like this and see if the pattern breaks. Once you suspect a pattern won’t break, you can try to use logic to prove it’s unbreakable.
After a chart like this one, or possibly a longer one (I’ve made charts 500 to 1,000 entries long in code just to see if a suspected pattern breaks), then you see that there’s a factor of 8 in every number found by subtracting 1 from the square of a prime greater than 3. And you try to prove that.
We want to show that every square of an odd number has a remainder of 1 when we divide by 8, so let’s make it simpler. Odd numbers are represented as 2n+1 and we remind ourselves of what we get when we square them:
Now we just have to show that this always has a factor of 8 and we’re done!
First we will factor out a 4, which gives us two of our needed three 2s (2 x 2 = 4):
Now we will factor the second part of the term:
So our factors are: 4, n, and n + 1.
Notice that n and n+1 are consecutive integers. That means that no matter what value n has, either n or n+1 is even. If n = 7, n + 1 = 8. If n = 11, n + 1 = 12. Always, always, always, either n or n + 1 must be even, and therefore divisible by 2.
So now we have shown that for every situation of:
There is a factor of 3 by virtue of one of the factors of p squared minus 1 always being divisible by 3.
And we have shown that there is a factor of 8, by virtue of the fact that an odd square minus 1 factors into 4, n, and n+1, and either the n or the n+1 gives us a factor of 2.
Because 4 x 2 = 8, we’re done.
So now we have finished our proof and solved our problem!
Every prime greater than 3, when we square it, is in fact 1 mod 24 — it has a remainder of 1 when we divide by 24.
This is true 100% of the time, and we can know this with total certainty.
Prime numbers are the building blocks of mathematics, which is the language of the universe, and we now know something really cool about what happens when we square them.
I love that.
I love number theory!
And if anyone except my extremely tolerant friends
and actually read to the end, thank you!For the Maths Nerds
For the math lovers (or even the math-curious types), here’s what one possible proof looks like when not trying to sneak in some extra understanding and explaining each step for a largely math-phobic audience:
And another one, the promised Putnam practice problem:






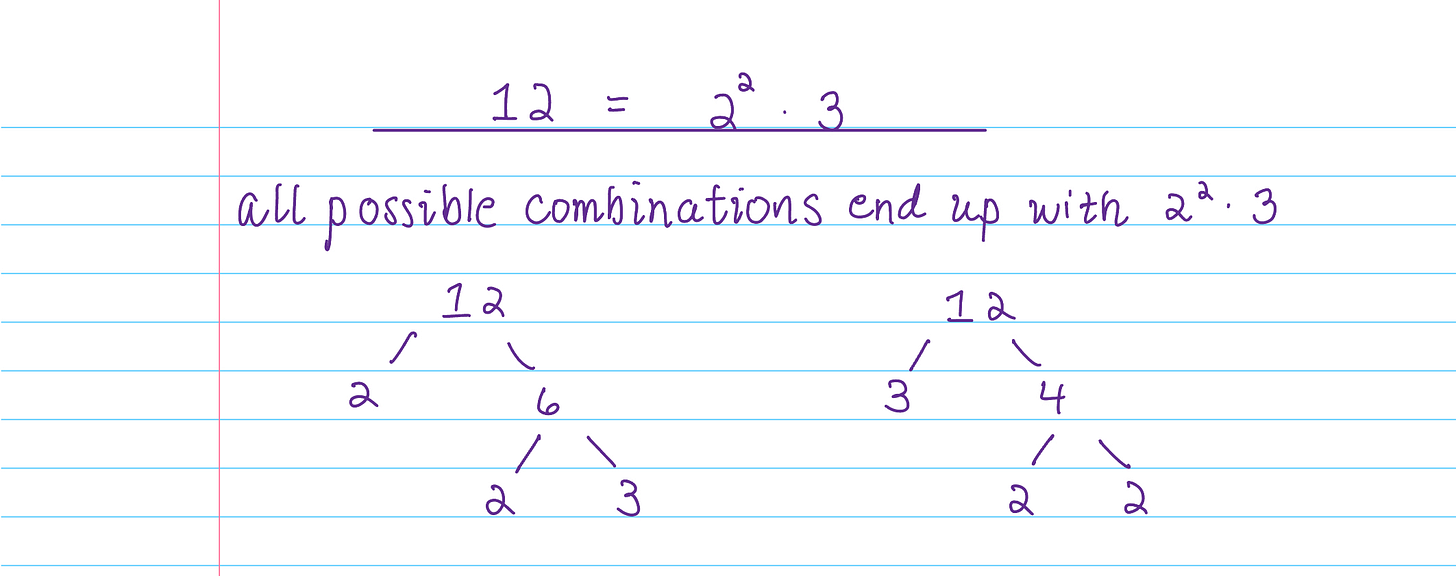
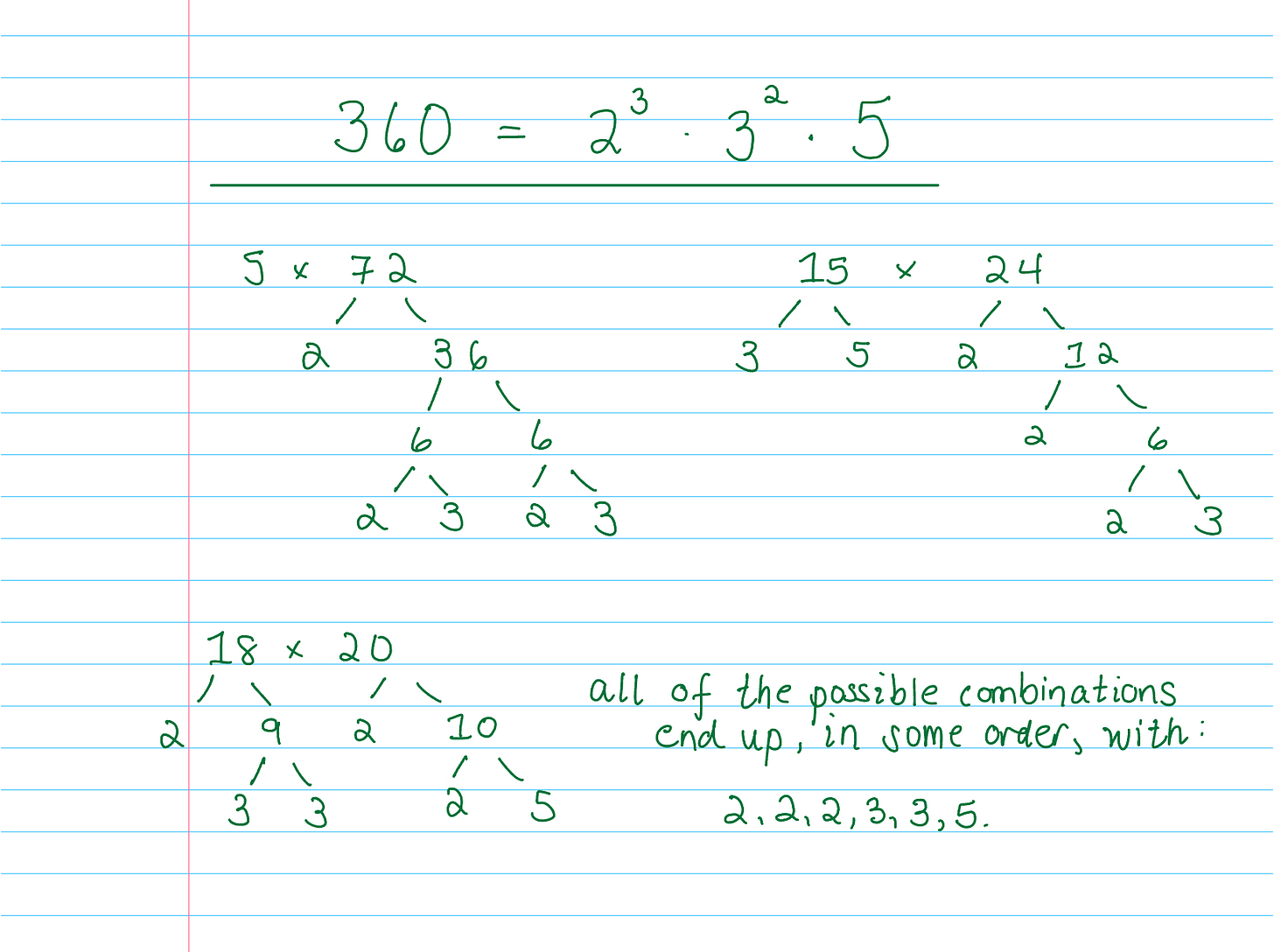


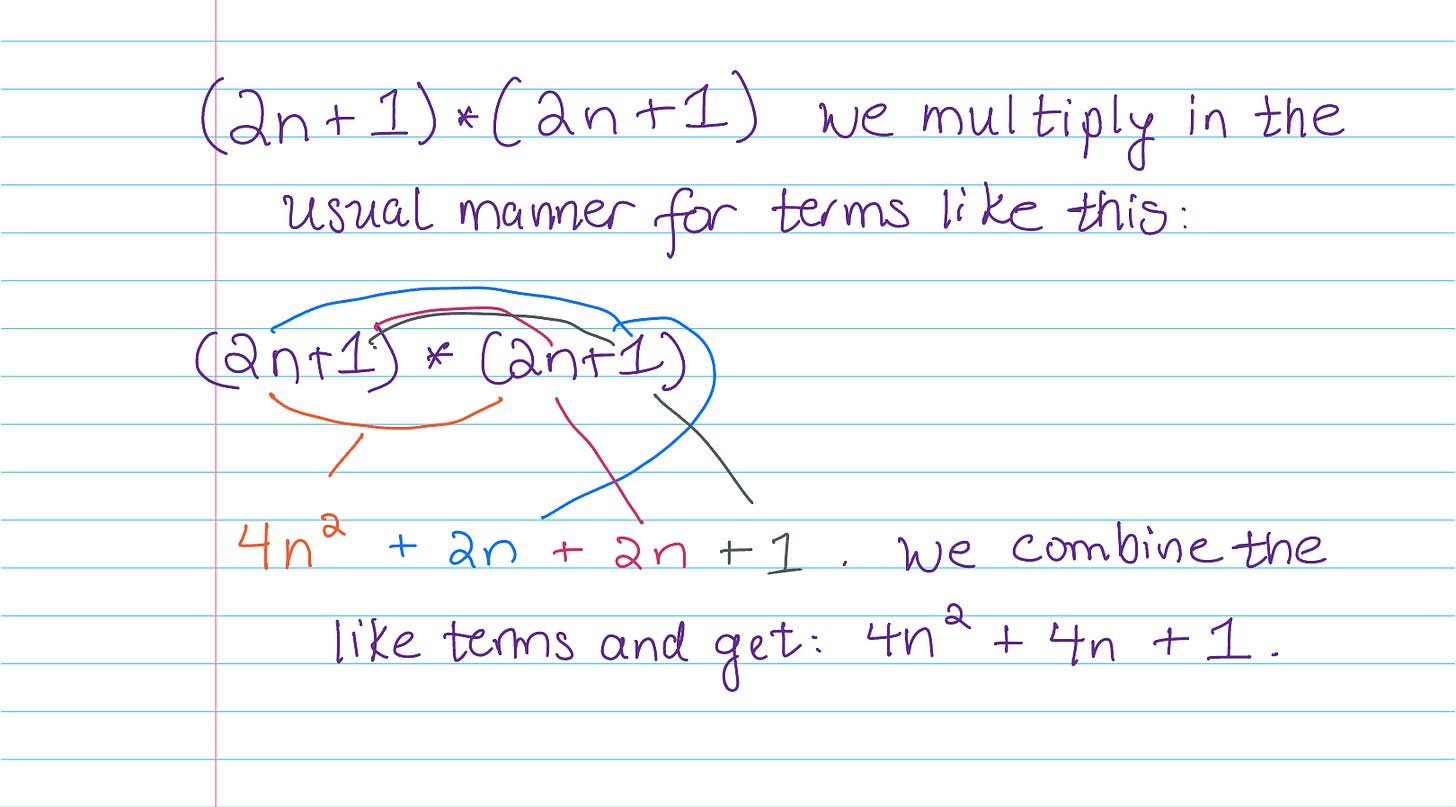

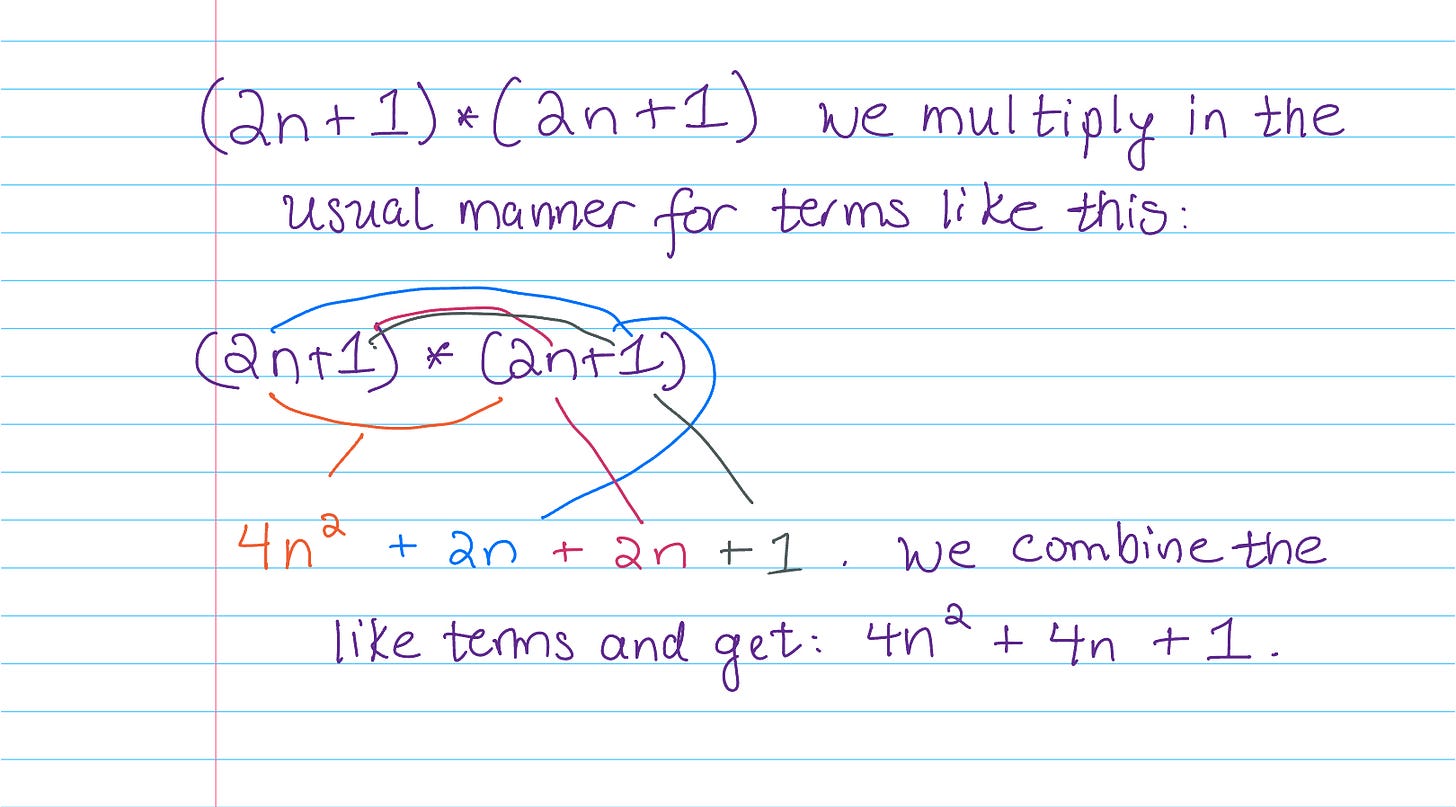



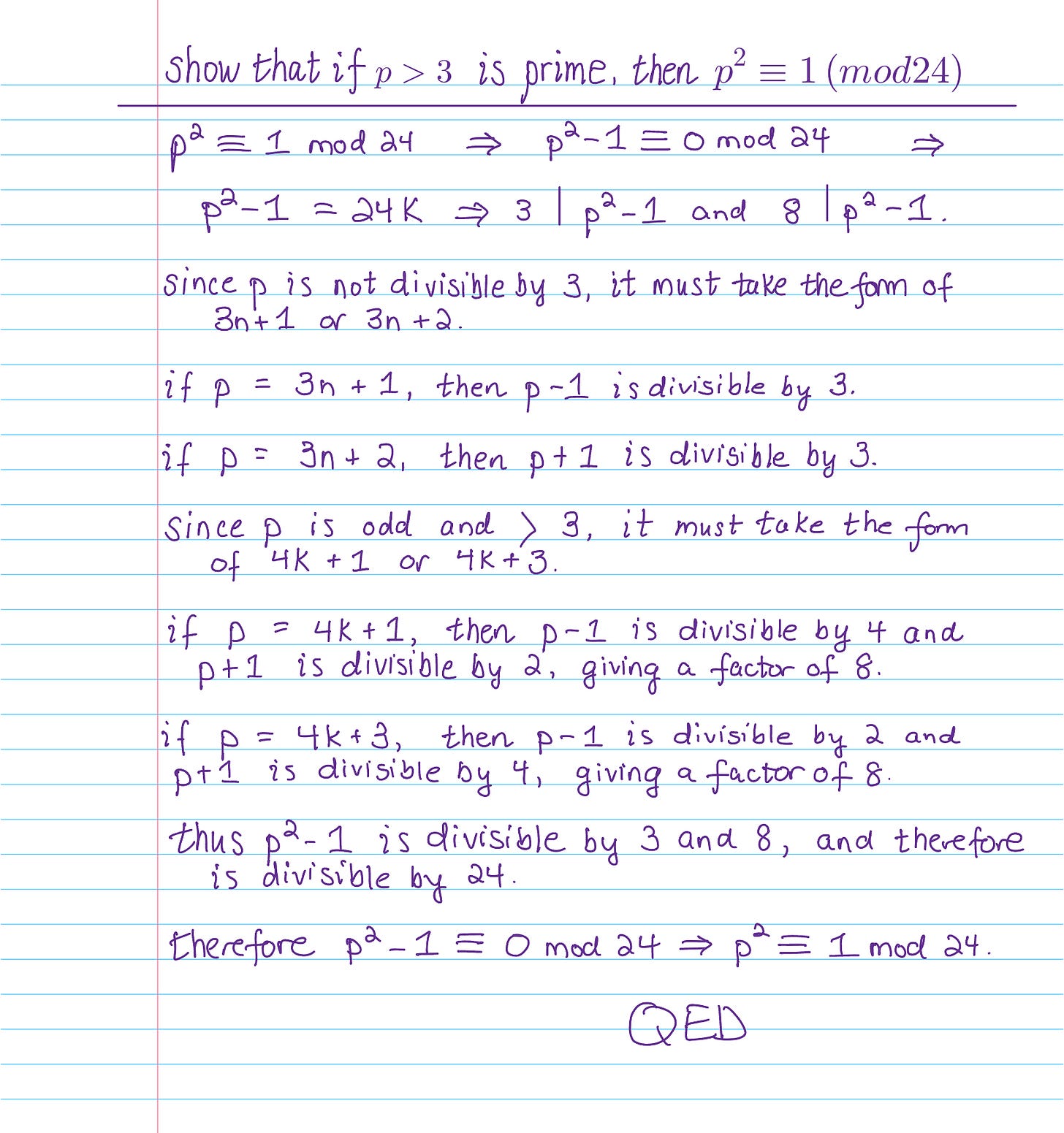
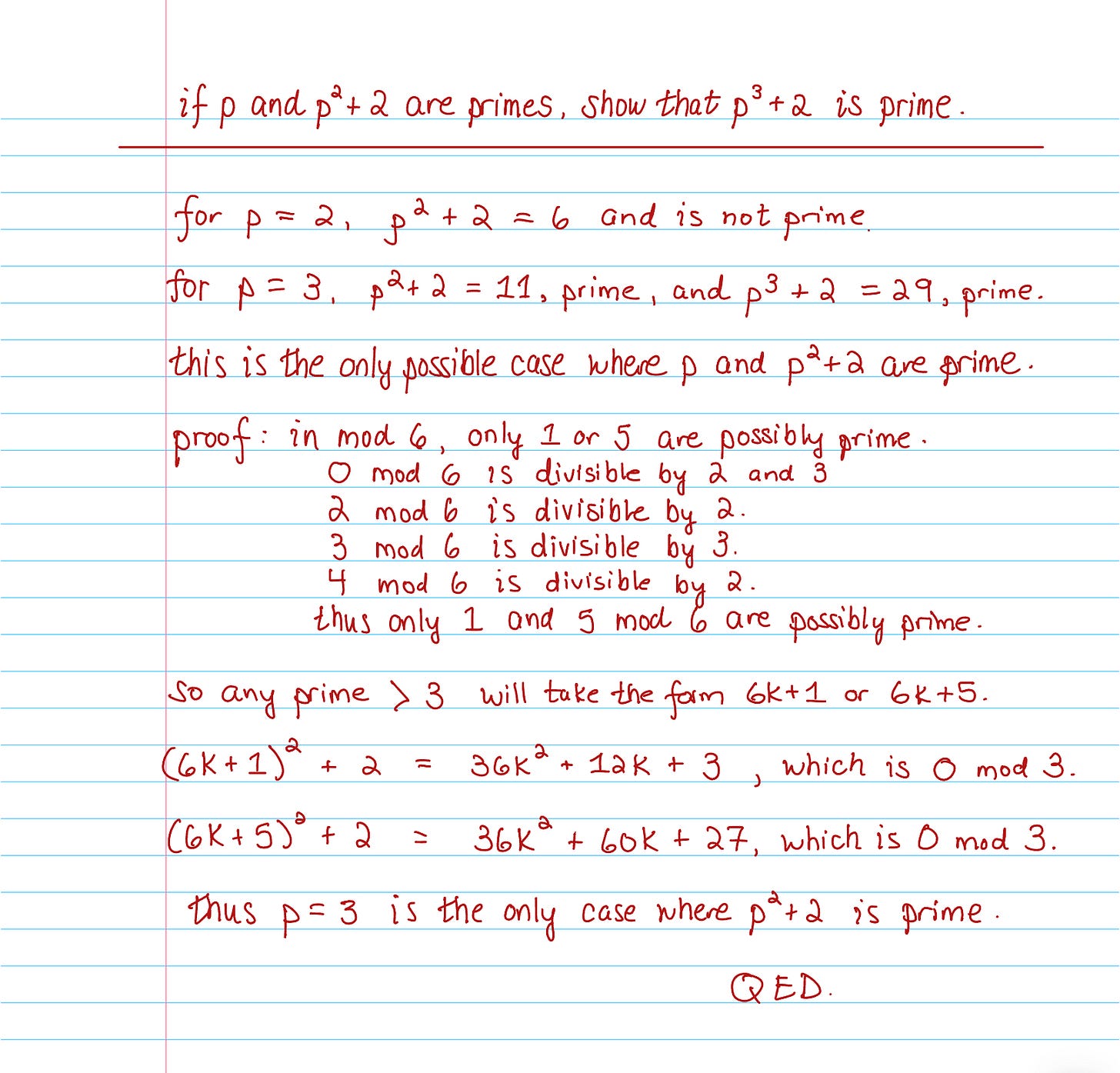
Disclaimer:
I’m not a math person so I apologize in advance if this joke is inaccurate and/or not funny.
PSA: Eating too much cake is the sin of gluttony. However, eating too much pie is okay because the sin of pi is always zero.
Hi, many thanks for the wonderful post, it made my day! An alternative proof for the factor 8, possibly easier to understand for non-math people, is analogous to your proof for the factor 3.
p-1, p, p+1, p+2 are 4 consecutive numbers, so one of them is divisible by 4, and one other is divisible by 2. Since both p and p+2 are odd, that means that p-1 and p+1 together have a factor of 8.