In the history of philosophy, there are many fun, interesting, classic problems that serve as the source of myriad discussions.
One set of these is Zeno’s Paradoxes.
Zeno was fascinating, and I’m tempted to give you three paragraphs of background here, but instead I encourage you to take the initiative to investigate him for yourself. Write me an email if you do; I love talking about this stuff!
I don’t remember when or where I first heard the paradox of halfway points (known to wiser minds as the “Progressive Dichotomy Paradox”), but I remember pondering it as a child of perhaps eight or nine years. I was a voracious reader at that age, so I assume I read about it somewhere, but I don’t know that for sure. A neighbor or a friend’s parent may have told me about it.
The following passage is copy and pasted from the Internet Encyclopedia of Philosophy (IEP) (emphasis added):
In his Progressive Dichotomy Paradox, Zeno argued that a runner will never reach the stationary goal line on a straight racetrack. The reason is that the runner must first reach half the distance to the goal, but when there he must still cross half the remaining distance to the goal, but having done that the runner must cover half of the new remainder, and so on. If the goal is one meter away, the runner must cover a distance of 1/2 meter, then 1/4 meter, then 1/8 meter, and so on ad infinitum. The runner cannot reach the final goal, says Zeno. Why not? There are few traces of Zeno’s reasoning here, but for reconstructions that give the strongest reasoning, we may say that the runner will not reach the final goal because there is too far to run, the sum is actually infinite.
Here’s a diagram I made to try to make this a bit clearer by giving you a visual.
Zeno’s conclusion, that the final goal is not reachable, is obviously false, and yet it can be hard to explain why.
I’m going to show you several ways to understand it.
One Solution to Zeno’s Paradox
In mathematics, one way that you can immediately end any argument is to find a contradiction. Mathematics is all about logic, and any contradiction you can find in your interlocutor’s premise automatically wins the argument for you.
I had the Zeno discussion in a classroom once. I proposed that we phrase it as being, instead of a runner, about an individual crossing a room with a chalkboard, like the one we were in.
So one way to solve Zeno’s paradox would be to simply cross the room and write on the chalkboard:
I’m here. Proof By Contradiction!
That may feel a little like a cheat, but it isn’t. It proves the premise—that you can’t cross the distance at all—to be false. And that’s enough to be getting on with, to send Zeno back to his drawing board.
The Standard Solution
Mathematics provides us with the solution, as it does to so much in life.
In mathematics, an infinite sequence is a sequence of numbers in a particular pattern that goes up to infinity.
Zeno’s paradox describes an infinite sequence.
By covering half the distance, and then one fourth of the distance (half of the half that remains), and then one eighth of the distance (half of the half of the half that remains), and so on, you get a sequence that looks like this:
1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256…..and so on, to infinity.
An infinite series is the sum of an infinite sequence. It’s the solution to:
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256….and so on, to infinity.
You may be wondering how it’s possible to find this solution, since it goes on to infinity.
It’s so cool! Let me show you!
I’m going to show you a couple of different ways to look at it, so hopefully one way or another will give you a light bulb moment.
One Way to See the Standard Solution
One way is to look at the fractions as decimals.
1/2 = .5
1/4 = .25
and so on.
So that gives us this:
1/2 + 1/4 = .5 + .25 = .75
1/2 + 1/4 + 1/8 = .5 + .25 + .125 = .875
1/2 + 1/4 + 1/8 + 1/16 = .5 + .25 + .125 + .0625 = .9375
1/2 + 1/4 + 1/8 + 1/16 + 1/32 = .5 + .25 + .125 + .0625 + .03125 = .96875
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 = .5 + .25 + .125 + .0625 + .03125 + .015625 = .984375
And so on, with each step moving us a bit closer to….what? The answer is approaching something—do you see it yet?
Another Way to See the Standard Solution
You probably remember from algebra that you can do anything you like to any equation, as long as you do it to both sides. Let’s look at this as an equation.
But first, a reminder about exponents.
When you raise a number to an exponent, you are multiplying it times itself in a particular way. A number squared (raised to the exponent of 2) is the number times itself once, so it’s two of that number, multiplied together. Writing it out to make it clearer:
Looking at our infinite sequence again, which we want to turn into an infinite series by finding the sum, do you notice something? The denominator of each fraction is a power of 2.
Now let’s turn this into an equation and see if we can use algebra:
Is there a way to take that equation and actually find the answer? Find the sum? There is! We have a formula that works because this is a geometric series. I’m going to show you the formula, and then I’m going to show you part of why it works. (A full explanation would lose a lot of readers, but if you’d like to see it, comment and I’ll do an addendum later.)
The formula is:
What is a common ratio?
All this means is that you can find (or spot just by looking) the relationship of each term to the next. Zeno gives us the common ratio in his discussion of the problem.
From 1/2 to 1/4 to 1/8 and so on, each is half of the previous. Remember that, in word problems, of means multiply!
Half of a thing, means multiply the thing by half to find the answer using math.
So our common ratio is 1/2.
(In case you doubt me—which you should, always ask for mathematical proof—1/2 times 1/2 = 1/4. 1/4 times 1/2 = 1/8. You can see that if you look at our series, each term is 1/2 times the previous term.)
Before we use the formula to get our answer, here’s a partial explanation of why it works (taken from here). Remembering that in algebra we can do anything we want, as long as we do it to both sides:
Using the Formula
Another Way to See It
Here’s a square cut into portions, each the same size as the fractions in our series. You can see that it leads to one complete, fully intact square.
By the way — the math you just learned?
It’s taught in second semester calculus courses.
Mathematics really is nowhere near as difficult as our culture makes it out to be. Patience, persistance, and a teacher who cares about teaching are all you really need.
The Deepest Lesson of Zeno’s Paradox
The deepest lesson Zeno’s paradox is that problems are usually solvable—but sometimes you have to step outside the paradigm that described the problem to do so.
If you do step outside the paradigm, you might find a mathematically rigorous and airtight solution, like the math to sum an infinite series.
Or you might find something that feels a little more uncertain, like crossing the room to write “proof by contradiction” on the board.
But either way, you learn something new.
Most problems are solvable, but we may have to—forgive me the cliche, please—step outside our usual boxes.
Happy Monday, Y’all!
Housekeeping: paid subscribers can leave comments on most posts. Email hollymathnerd at gmail if you can’t afford a paid subscription and I’ll give you one.







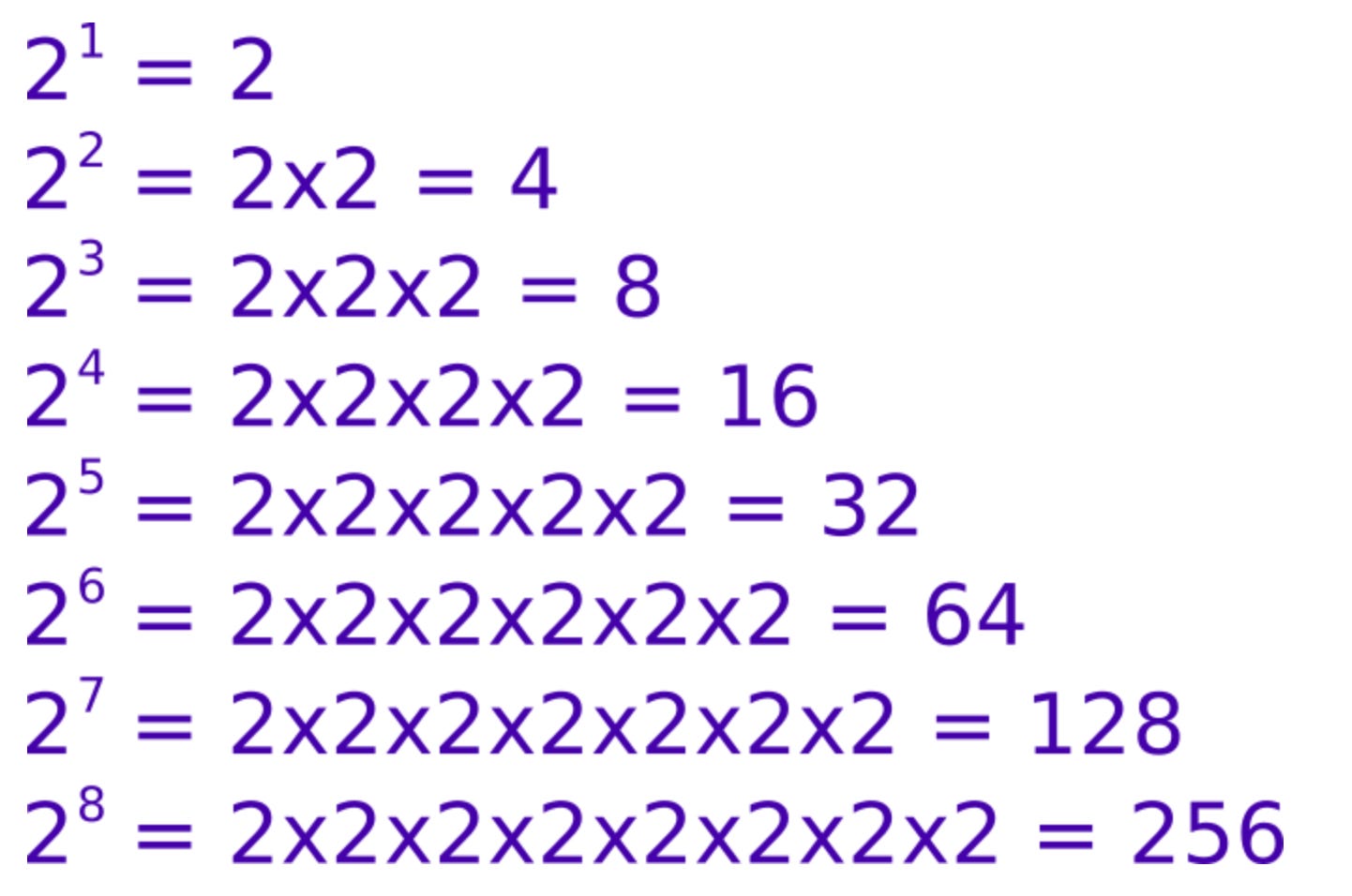





This is a great post! Nerdily enough, the first I ever heard of this supposition was at the end of a Star Trek novel, where one of the characters reaches "infinite speed," which led to a discussion of why there cannot ever be a "warp 10." During this discussion, two characters bring up the notion of something never reaching its destination if it only goes half the required distance over and over again. I didn't know it was called Zeno's Paradox until today.
I remember thinking then as I do now that this conflates two separate actions. All this proves is that any discrete distance (or number) can be divided in half. Dividing something in half and traversing a distance in space are two different things. Just because it's possible to go half of any distance does not mean that the full distance cannot be reached! It imposes an artificial limiter (only go half) on the action of travelling, which doesn't make sense to me in reality.
Thanks for engaging my brain this morning, Holly! :)
This is delightful - so much so I've just passed it onto my engineer partner for delectation & amusement.
Also brings back memories of high school calculus, where I was taught Zeno's Paradox in the form of the fable of Achilles & the Tortoise (Achilles never catches the tortoise, for the same half-way and half-again reasoning). I was then taught to solve it quite similarly to what you've done here.